Perimeter and Area of an Arch

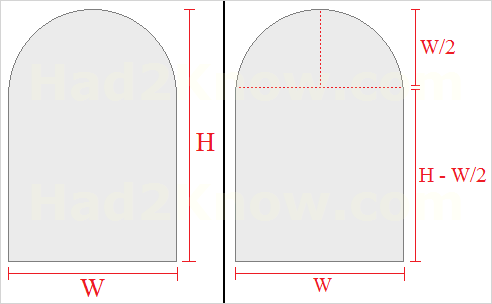
Arches are popular shapes in the construction of windows and doorways. In architecture, most arches are formed by appending a semi-circle to a rectangle so that the ends are flush. You can calculate the area and perimeter of an arch as long as you know the total height (H) and total width (W) of the shape. The formulas for area and perimeter are described below; you can also use the convenient arch calculator.

Area

If the total height is H and the total width W, then the rectangular part of the arch has dimensions W by H - W/2. The semi-circle has a radius of W/2. You can find the total area of the arch by adding the area of the rectangle and half-circle:

Area = W(H - W/2) + (π/2)(W/2)²
= WH - (1/2 - π/8)W²

Perimeter

The perimeter of an arch is equal to the sum of the three sides of the rectangle plus the half-circumference of the semi-circular portion. The formula is

Perimeter = W + 2(H - W/2) + πW/2
= 2H + πW/2

Example

An arch has a height of 15 meters and a width of 9.5 meters. What are the area and perimeter of the shape?

First, we have H = 15 and W = 9.5. Using the area formula yields

Area = (15)(9) - (1/2 - π/8)(9.5)²
= 135 - 0.107301(90.25)
= 125.316 square meters

And using the perimeter formula yields

Perimeter = 2(15) + π(9.5)/2
= 30 + 14.9226
= 44.9226 meters

Special Cases

There are many arches whose area and perimeter are equal. For example, an arch that is 4 units high and 4 units wide has an area and perimeter of 8 + 2π.

An arch where W = 8 and H = 16/3 - 2π/3 also has equal area and perimeter.

You can find many more sets of dimensions by setting the equations for area and perimeter equal to each other, plugging in a value for W, then solving for H.

© Had2Know 2010