Area of a Circular Segment

Circular Segment Area Calculator

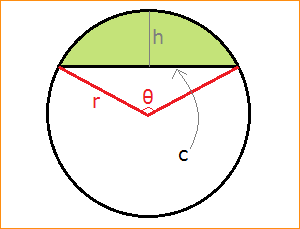
In geometry, a circular segment is a piece of a circle bounded by a circular arc and a chord. Segments arise in many practical situations, for example, if a cylindrical tank is laid on its side and partially filled with water, the cross-sectional shape of the water will be a circular segment. If you dip a circular cookie in chocolate coating, the chocolate covered part will be in the shape of a segment.

To compute the area of a segment, you must know two of the following four values:

• length of the chord c
• height of the segment h
• radius of the circle r
• angle of the segment θ

The chord length, height, radius, and angle are interrelated by several equations:

c = 2r*sin(θ/2) = 2*sqrt(2rh - h²)
h = r - sqrt(r² - c²/4) = r - r*cos(θ/2)
θ = 2*arccos(1 - h/r) = 2*arcsin(c/(2r))
r = c²/(8h) + h/2

Area of a Segment

There are four equations for the area of a circular segment depending on which two values you know. If you know r and one of c, h, or θ, then the first three equations are:

A = r²arcsin(0.5c/r) - 0.5c*sqrt(r² - c²/4)
A = r²arccos(1 - h/r) - (r-h)sqrt(2rh - h²)
A = 0.5r²[θ - sin(θ)]

where the θ, arcsin, and arccos are in radians, not degrees. If you know the values of c and h, then the fourth area formula is

A = [c²/(8h) + h/2]²arccos[(c²-4h²)/(c²+4h²)] - c³/(16h) + ch/4

where again, arccos is in radians.If the segment is larger than a semi-circle and you are using either the first or third equation, you need to add (π/2)r², the area of a semi-circle. The second and fourth equations work for any height, so no adjustments are necessary if the segment is more than half of the circle.

Don't worry about adding (π/2)r² if you use the calculator above, it will make the adjustment when you check "yes."

Also, if you enter the value of θ in the calculator, use degrees rather than radians. The calculator will make the conversion to radians for you.

There is also a fifth area formula, an approximation version of the second area equation. For best results use this estimation equation only when the height of the segment is less than the radius:

A ≈ (4h²/3)sqrt(2r/h - 0.605)

Example:

Suppose a cylindrical tank is 12 feet long and 2 feet in diameter. The tank is laid on its side and filled with water to a height of 7 inches. Given that the volume of water in the tank is equal to the length of the tank times the cross-sectional area of the water, find the tank's volume.

First, we are given r = 1 foot, since the radius is half the diameter. Second, we have h = 7/12 feet, since we must convert inches to feet. Using the second formula for the area of a circular segment gives us

A = (1)arccos(1 - 7/12) - (1 - 7/12)sqrt(14/12 - 49/144)        use arccos in radians
= 1.14102 - 0.37877
= 0.76225 square feet.

So the volume of water in the tank is 12(0.76225) = 9.147 cubic feet.

How the Formulas are Derived

Each of the three area formulas involves subtraction. This is because the area of a circular segment is the area of a sector minus the area of a triangle.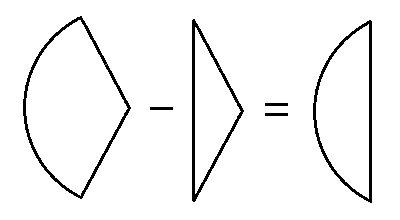

© Had2Know 2010