Barrel Dimensions Calculator

A barrel is shaped much like a cylinder except that the middle bulges outward. If you know the radius r of the ends of the barrel, the radius R at the middle of the barrel, and the height H, then you can plug these variables into a formula to compute the approximate volume of the barrel.

There are two equations for estimating the volume of a barrel: one that assumes the shape of the barrel's side curve is a parabolic arc, and a simplified formula.

Likewise, if you know the volume of the barrel and two out of three values of the dimensions r, R, and H, then you can use algebra to find the missing dimension.

The calculator on the left computes the missing measurement when you select the equation type, input the volume, and input two of barrel's three measurements. To compute the volume from the three dimensions, use the Barrel Volume Calculator.

Parabolic Barrel Volume Formula

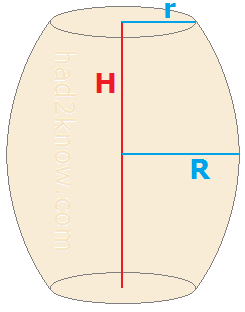
If you assume that the curve formed by the side of the barrel is the arc of a parabola, then the volume equation is

V = πH(3r² + 4Rr + 8R²)/15

Solving this equation for r, R, and H gives you

r = sqrt[5V/(πH) - 20R²/9] - 2R/3

R = sqrt[15V/(8πH) - 5r²/16] - r/4

H = 15V/[π(3r² + 4Rr + 8R²)]

Simplified Barrel Volume Formula

The next volume formula is more commonly used and gives greater weight to the middle radius of the barrel:

V = πH(r² + 2R²)/3

Isolating r, R, and H gives the equivalent expressions

r = sqrt[3V/(πH) - 2R²]

R = sqrt[3V/(2πH) - r²/2]

H = 3V/[π(2R² + r²)]

Example

Marcy has a barrel whose volume is 45,000 cubic inches. The height of the barrel is 29 inches and the radius at the ends of the barrel is 12 inches. What is the middle radius?

Using the simplified volume formula gives

R = sqrt[3*45000/(2*π*29) - 12*12/2]
= sqrt(668.8937)
= 25.863 inches

© Had2Know 2010