Equation for the Shape of a Hanging Rope, Cable, or Chain
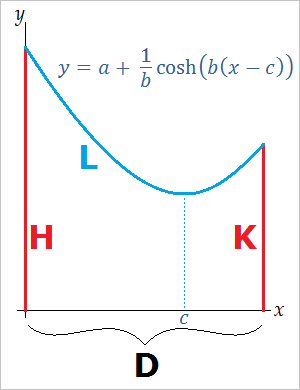
When the ends of a rope, cable, or chain are attached to the tops of two poles, the suspended cable forms the shape of a catenary. Catenaries have equations of the form
y(x) = a + (1/b)cosh(b(x-c)),
where a, b, and c are constants. The function cosh(x) is (ex + e-x)/2. If you know the height of the two poles, the distance between them, and the length of the chain, you can solve a system of equations in the variables a, b, and c to find the explicit equation of the catenary. You can also use the catenary equation calculator on the left.
First, denote the height of the taller pole by H, the height of the shorter pole by K, the distance between the poles by D, and the length of the chain by L. To simplify the calculations, we assume that the taller pole lies on the y-axis as in the figure below. If we plug 0 and D into the equation
y(x) = a + (1/b)cosh(b(x-c)), we obtain
H = a + (ebc + e-bc)/(2b)
K = a + (eb(D-c) + e-b(D-c))/(2b)
If we set L equal to the arc length integral of y(x) between 0 and D, we get
L = (eb(D-c) - e-b(D-c) + ebc - e-bc)/(2b)
This system of equations cannot be solved with straight-forward algebra, but you can use a graphing calculator, numerical approximation methods, or the equation solver above to find the values for a, b, and c.
The value of c determines where the vertex or lowest point of the hanging cable is. If c is less than D, the chain has a minimal point between the two poles. If c is greater than or equal to D, the cable's lowest point is at the top of the shorter pole. This occurs when L is very short and the chain does not dip down very far.
If the poles are of equal height, then c is equal to D/2.
If L2 = D2 + (H-K)2, then the cable makes a straight line between the two poles.
© Had2Know 2010
