Home » Academics » Chi-Square Test Calculator

Chi-Square Test Calculator

The chi-square distribution with d degrees of freedom gives distribution of the sum of the squares of d normally distributed random variables. Its probability density function is

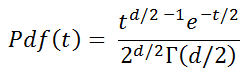
The chi-square distribution is used in hypothesis testing to determine the likelihood of the null hypothesis--that the observations are consistent with a theoretically assumed distribution. The test statistic is χ² is

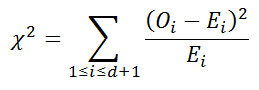
where O_i is the number of observations in group i, and E_i is the expected number in group i. The degrees of freedom is usually 1 less than the number of observations. In practical applications, researchers often reject the null hypothesis if the probability is less than a given threshold, such as 0.05 or 0.01.

Chi-Square Test Calculator

Use the calculator above to compute the chi-square test statistic and probability for a set of observations. (You can also use a chi-square table.)

Example

A researcher operates under the assumption that 40% of people in a given area (between the ages of 18 and 65) are employed full-time outside the home, 35% are employed part-time outside the home, and 25% fall into other categories. This assumption is the null hypothesis. He samples 320 people and comes up with the following observed data:

Full-time outside the home: 113
Part-time outside the home: 117
Other: 90

The expected data is

Full-time outside the home: 320(0.40) = 128
Part-time outside the home: 320(0.35) = 112
Other: 320(0.25) = 80

The degrees of freedom is 2 and the chi-square value is

(113-128)²/128 + (117-112)²/112 + (90-80)²/80 = 3.23102

The probability of obtaining these observations, given a theoretical distribution of 40%-35%-25%, is 0.198789. This is not low enough to reject the hypothesis; he has no reason to assume that the underlying distribution is not 40%-35%-25%.