Copyright © Had2Know 2010-2026. All Rights Reserved.
Terms of Use | Privacy Policy | Contact
Site Design by E. Emerson
Chi-Squared Distribution Random Number Generator
The chi-squared distribution with k degrees of freedom, denoted χ2k is the distribution of the sum of the squares of k normally distributed random variables (with mean 0 and variance 1). Chi-squared distributions are often encountered when studying multiple data sets whose elements come from a normal distribution. Statistical hypothesis testing is another application. You can use the calculator below to generate random variables from a χ2k distribution.
The PDF of the chi-squared distribution is
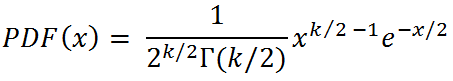
mean = k
mode = 0 if k < 3, k-2 otherwise
variance = 2k
skew = sqrt(8/k)
There is no closed form of the median of the χ2k distribution, Med(k). However, it can be approximated with the following equation:
Med(k) = 0.455 for k = 1,
Med(k) = 1.386 for k = 2,
Med(k) = k(1 - 0.224/k)³ for k > 2
© Had2Know 2010
