Copyright © Had2Know 2010-2025. All Rights Reserved.
Terms of Use | Privacy Policy | Contact
Site Design by E. Emerson
Circles Inscribed Within an Annulus
An annulus is a ring shaped figure formed by two concentric circles with differing radii. Within the ring-shaped area of the annulus you can inscribe a ring of smaller circles tangent to the border of the annulus. (See figure below.)
The maximum number of such circles depends on the inner and outer radii of the annulus. The diameter of these circles is the difference between the outer and inner annulus radii.
You can use the calculator on the left to compute the maximum number of circles that can be inscribed as well as their radius. To compute it by hand, you can also use the mathematical formula discussed below.
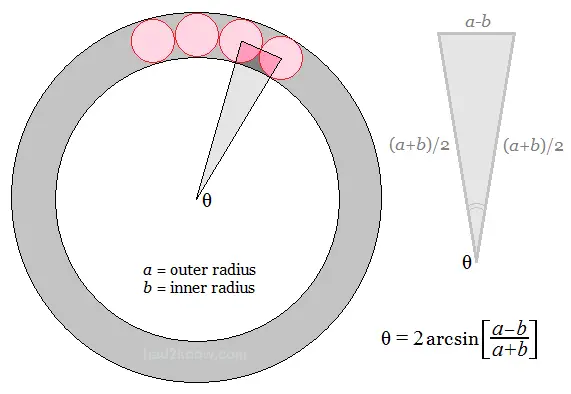
The smallest angle of this triangle is
θ = 2*arcsin[(a-b)/(a+b)].
The number of inscribed circles is thus
N = 2π/θ (θ measured in radians) or
N = 360/θ (θ measured in degrees)
If N is not an integer, round down to the nearest whole number.
Example: An annulus has an outer radius of 50 and an inner radius of 43. The angle θ is computed to be
θ = 2*arcsin[(50-43)/(50+43)]
= 2*arcsin(7/93)
= 8.633336 degrees
Next, N is computed:
N = 360/8.633336
= 41.698829
= 41.
This means that a maximum of 41 circles can be packed inside the annulus.
© Had2Know 2010
