How Many Digits Does a Large Exponent Have?

Calculating the Number of Digits in a^b

For small exponential expressions such as 5⁸, you can determine its number of digits simply by evaluating the expression and counting the digits. For instance, 5⁸ = 390625, an integer with 6 digits.

However, it is more challenging to count the number of digits in a large exponent such as 47¹⁰⁰⁰⁰. If you try to evaluate it on a standard calculator, you will get an overflow error message since it is a number with 16721 digits.

Rather than count the number of digits in a larger exponent, it is easier to calculate their number. You can do this using logarithms and the explanation below, or the calculator at left.

Using Log₁₀ to Calculate the Number of Digits

The formula for the number of digits D in a^b is

D = 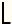1 + Log₁₀(a^b) 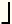= 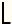1 + (b)Log₁₀(a),

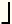where ⌊ ⌋ is the floor function. Logarithm base-10 appears in this formula because we use a base-10 number system.

To see why the above formula works, consider the smallest 4-digit number and the smallest 5-digit number--1000 and 10000. Notice that 1000 = 10³ and has 4 digits, and Log₁₀1000 = 3. Similarly, 10000 = 10⁴ and has 5 digits, and Log₁₀10000 = 4. The number of digits in 1000 and 10000 is one more than their logarithms.

Now consider a number between 1000 and 10000, for example, 5481. This is a number with 4 digits and Log₁₀5481 = 3.7389. The number of digits in 5481 is equal to 3.7389 rounded up to the nearest whole number.

Thus, to compute D, you take the logarithm of the number in base-10, add 1, and then round down to the nearest integer.

Example: Calculate the number of digits in 7777⁸⁸⁸⁸.

D = 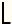1 + Log₁₀7777⁸⁸⁸⁸ 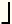= 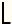1 + 8888Log₁₀7777 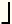= 34582.

© Had2Know 2010