How to Compute Square Roots by Hand

Prior to the widespread use of calculators, most people calculated square roots by looking up the values in a table or computing them by hand in a process similar to long division. The technique of calculating square roots by hand is no longer taught in schools, but it is still of interest to the mathematically curious. If you follow the tutorial below, you can hand-compute square roots for numbers of any size to any level of accuracy.

Step 0: Group the digits of the number into pairs, starting from the right side. If the number has an odd number of digits, the first number will be by itself.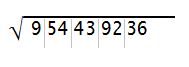
Step 1: Starting at the left, take the square root of the first group of numbers (may be a one- or two-digit number) and round down to the nearest whole digit if you get a decimal. In this example, the first group of numbers is 9 and its square root is exactly 3. Write this digit above the first group of digits, above the radical bar. Square the digit, write that number below the first group of digits, and subtract. Bring down the next pair of digits.
Step 2: Call the new number at the bottom C and the digit above the radical bar P. You want to find the largest digit N such that (20P+N)N ≤ C. To find a candidate for N, compute C/(20P) and round down to the nearest whole digit. Test your candidate to make sure it is the largest digit that satisfies (20P+N)N ≤ C; you may have to adjust it up or down. Once you find N, write it above the second pair of digits, above the radical bar. Then compute (20P+N)N, write it below C, subtract, and bring down the next pair of digits.
Step 3: Repeat the process outlined in Step 2, except this time your value of C is the new number at the bottom (5443 in this example), and your value of P is the new number above the radical bar (30 in this example). For instance, if C = 5443 and P = 30, you first compute 5443/(30*20), which equals 9 when rounded down. Then you check whether (30*20+9)(9) is less than or equal to 5443. It turns out the answer is no, so you then check 8. Since (30*20+8)(8) is less than 5443, you write 8 above the radical bar. Evaluating (30*20+8)(8) gives you 4864, and 5443 - 4864 = 579. When you drop down the next two digits, you get 57992.
Step 4: Repeat the above process for each pair of digits as you work your way to the right. In each step the values of C and P will get larger, but remember that N must always be a digit (a number between 0 and 9).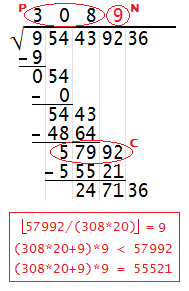
Step 5: If your original number turns out to be a perfect square, the process will terminate when you get a difference of 0 at the end. In this example, it turns out that 30894² = 954439236 exactly. If your number is not a perfect square and you want to compute its square root to the nearest tenths or hundredths, you must append several pairs of zeros to the right of the final digit, and continue the process.

© Had2Know 2010