Equation of a Conic Section Through Five Points

Conic Section Equation Calculator

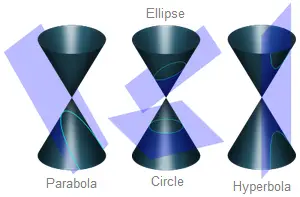
A conic section is a curve generated by slicing a double napped cone with a plane. The four conic section curves are the circle, ellipse, parabola, and hyperbola. Circles and ellipses are formed when a plane cuts the cone at an angle that is less than the angle of the cone's sides. A parabola is formed by cutting the cone at an angle equal to the cone's sides, that is, the plane is parallel to the side.

A hyperbola occurs when the plane is parallel to the vertical axis of the cone. Hyperbolic curves consist of two disjoint pieces that are mirror images. When the plane cuts straight through the vertical axis, the hyperbola degenerates into two intersecting lines.

The four curves are shown in the figure below:

General Equation of a Conic Section

In Cartesian coordinates, the general equation of a conic section is

Ax² + Bxy + Cy² + Dx + Ey + F = 0,

where not all of A, B, and C are equal to zero. Whether the curve is a hyperbola, parabola, ellipse, or circle depends on the value of the discriminant, B² - 4AC. The three cases are

B² - 4AC > 0, hyperbola
B² - 4AC = 0, parabola
B² - 4AC < 0, ellipse or circle (circle only if B = 0 and A = C)

Given five distinct points in the xy-plane, no more than three of which are collinear, there is a unique conic section that passes through the points.

How to Find A, B, C, D, E, and F

Suppose the coordinates of the five points are (m, n), (p, q), (r, s), (u, v), and (w, z). The equation of the conic section is found by calculating the determinant of a 6-by-6 matrix and setting it equal to 0. The matrix equation is:



The coefficients A, B, C, D, E, and F are found from the minors of the larger matrix. For example, suppose you want to find the equation of the conic section through the points (3, 3), (2, -1), (1, -2), (-2, 1), and (-3, -3). Computing the matrix determinant gives you conic equation

-1188x² + 1404xy - 1188y² + 0x + 0y + 8748 = 0.

Using a scientific calculator with GCD function, you can reduce the coefficients of the equation and simplify it as

11x² - 13xy + 11y² = 81,

which represents an ellipse centered at the origin. You can use the conic section calculator above the find the equation of a conic curve when you input the coordinates of five points.

© Had2Know 2010