Surface Area and Volume of a Conical Frustum

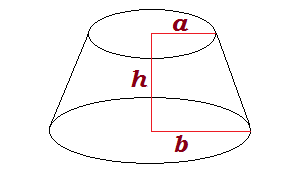
A conical frustum is a truncated cone. This solid geometrical shape is obtained by slicing the top off of a cone leaving a circular top. The resulting shape resembles a cylinder, except the bottom is wider than the top.

You can compute the volume and surface area of a conical frustum from its height, bottom radius, and top radius. The calculator below will compute the surface area and volume if you input values for the height and radii. You can also apply the formulas described below.

Volume of a Conical Frustum

Call the height of the frustum H, the top radius A, and the bottom radius B. The volume of the solid is given by the equation

Volume = (pi/3)H(A² + AB + B²).

Note: pi is the mathematical constant 3.14159265358...

Surface Area of a Conical Frustum

The surface area formula excluding both bases is

Surface Area = pi(A + B)sqrt[(B-A)² + H²].

The formula for its total surface area (including the bases) is

Surface Area = pi(A + B)sqrt[(B-A)² + H²] + pi(A² + B²)

Example

Suppose a conical frustum is 20 cm tall with a top radius of 5 cm and a bottom radius of 10 cm. So we have H = 20, A = 5, and B = 10. The volume is

(pi/3)(20)(5² + (5)(10) + 10²) = 3,665 cm³

The surface area (excluding the bases) is

pi(5+10)sqrt((10-5)² + 20²) = 971 cm²

© Had2Know 2010