Descartes' Theorem and Soddy Circle Radius Calculator for 4 Mutually Tangent Circles

If three circles are mutually tangent (osculating circles, or "kissing" circles), there is a circle in the interior that is mutually tangent to the three, as well as an exterior circle mutually tangent to the three.

Four mutually tangent circles are known as Soddy Circles, after the radiochemist Frederick Soddy who rediscovered Descartes' Theorem for finding the radii of these circles.

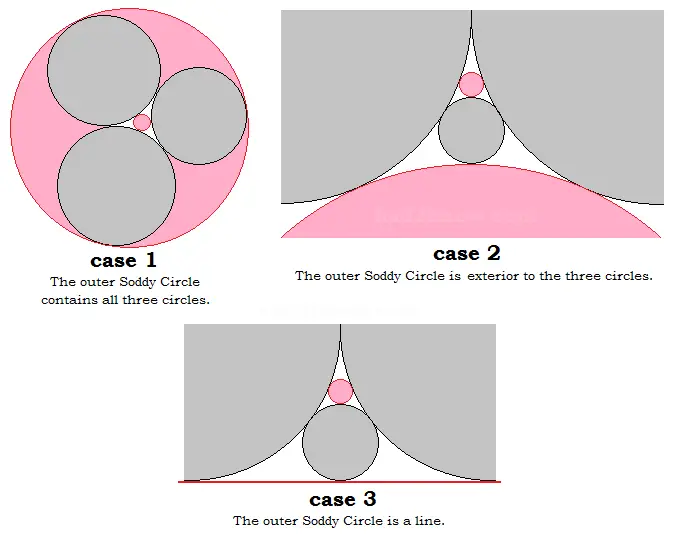
The diagram below shows three different cases of Soddy circles: (1) when the exterior fourth circle circumscribes the three circles, (2) when the exterior Soddy circle does not circumscribe the other three, and (3) when the outer Soddy Circle is a line (a circle of infinite radius). The gray circles are the three given osculating circles, and the pink circles are the possibilities for the fourth mutually tangent circle.

With the calculator on the left, you can input the radii of three mutually tangent circles and find the radii of the interior and exterior fourth circle.

Descartes' Theorem

Given three mutually tangent circles with radii A, B, and C, the radius X of the fourth Soddy Circle can be found by solving the equation

[1/A + 1/B + 1/C + 1/X]² = 2[1/A² + 1/B² + 1/C² + 1/X²]

This yields two solutions for X, corresponding to the interior and exterior fourth circles. The radii are

X_interior = ABC/[AB + BC + CA + 2√ABC(A + B + C)]
X_exterior = ABC/[AB + BC + CA - 2√ABC(A + B + C)]

If AB + BC + CA > 2√ABC(A + B + C), the exterior fourth circle is as in Case 2. If AB + BC + CA < 2√ABC(A + B + C), the exterior fourth circle is as in Case 1. If AB + BC + CA = 2√ABC(A + B + C), the exterior fourth circle is a line (Case 3).

© Had2Know 2010