Digamma Function Calculator

The digamma function, denoted by ψ, is the logarithmic derivative of the Gamma Function. That is,

ψ(z) = [Ln(Γ(z))]' = Γ'(z)/Γ(z).

Like the gamma function, the digamma function has its own interesting representations in terms of integrals and infinite sums. The simplest form of the digamma function is

ψ(z) = -(γ + 1/z) + Σ^∞_n=1 z/(n² + nz),

where γ is the Euler-Mascheroni constant 0.57721566490153286060651209... When z is a positive integer, you can evaluate ψ(z) directly with the formula

ψ(z) = -γ + Σ ^z-1_n=1 1/n.

When z is a half-integer, you can compute the digamma function with the formula

ψ(z + 1/2) = -γ -2Ln(2) + 2Σ ^z_n=1 1/(2n-1).

To find the value at negative half-integers, you can use these functional relations that hold for all values of z:

ψ(z + 1) = 1/z + ψ(z)
ψ(1-z) - ψ(z) = πcot(πz)

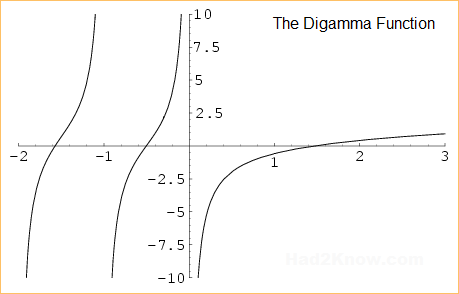
Special values of the Digamma Function

For some values of z, ψ(z) can be written in terms of γ, π, and natural logarithms. Some special values of the digamma function are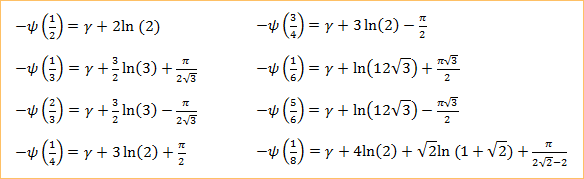

More Representations of the Digamma Function

Here are several other expressions involving the digamma function: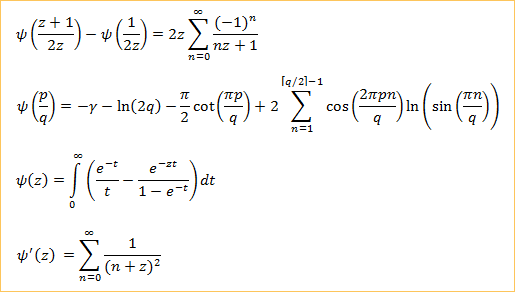

© Had2Know 2010