Copyright © Had2Know 2010-2025. All Rights Reserved.
Terms of Use | Privacy Policy | Contact
Site Design by E. Emerson
Surface Area and Volume of an Egg
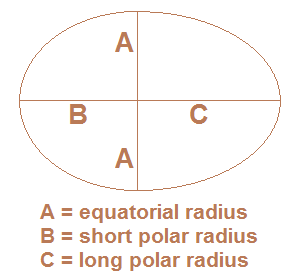
The two-dimensional shape of an egg can be drawn by joining two ellipses (ovals) at their minor axes. (See figure below the calculator.) A three-dimensional egg is obtained by rotating the two-dimensional egg shape along the major axis. If you know the width and length of the egg, you can find its volume and surface area using the formulas below. Or you can use the egg calculator below to find its measurements.
Volume of an Egg
The width of an egg is its equatorial diameter. Half of this diameter is the equatorial radius, which you can call A. The total length of the egg is its polar diameter. The distance from the equator to the nearest pole is the short polar radius of the egg; call this number B. The distance from the egg's equator to the farthest pole is the long polar radius; call this number C.The shape of an egg can be thought of as two halves of ellipsoids with different radius dimensions. One has radii of A, A, and B; the other has radii of A, A, and C. The volume is given by the formula
(1/2)(4π/3)A2B + (1/2)(4π/3)A2C
= (2π/3)A2(B+C),
where π is the geometrical constant 3.14159265358...
Surface Area of an Egg
The surface area formula for an egg requires the inverse trigonometric function arccos, often written as cos-1. If you use the arccos button on your calculator, make sure the mode is set to radians, not degrees. The formula for the surface area of an egg is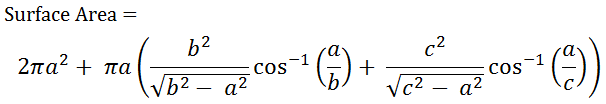
Example
Suppose an egg has an equatorial radius of 1.9 cm, a short polar radius of 2.2 cm, and a long polar radius of 3.2 cm. Then A = 1.9, B = 2.2, and C = 3.2. The volume of the egg is
(2π/3)1.92(2.2 + 3.2)
= 40.83 cm3.
The surface area is 58.64 cm.2
© Had2Know 2010
