Area and Perimeter of an Ellipse or Circle

In geometry, a circle is a special type of ellipse in which the length and width are equal. You may remember the formulas for the area and circumference of a circle from grade school:

Area = pi*R²
Circumference = 2*pi*R,

where R is the radius and pi is the mathematical constant 3.1415926... You can also write these equations in terms of the diameter D:

Area = pi*D²/4
Circumference = pi*D.

What you might not recall are the corresponding formulas for ellipses. Figuring the area and perimeter of elliptical shapes can prove useful in architecture and design, engineering, and many other fields. You can reference the formulas below, or use the circle and ellipse calculator on the left.

Area of an Ellipse

If an ellipse has a total length of A and a total width of B, then the area is given by the formula

Area = pi*(A/2)(B/2)
= pi*AB/4

Perimeter (Circumference) of an Ellipse

Unfortunately the formula for the perimeter of an ellipse is much more complicated than any of the formulas above. The exact perimeter is given by an integral that has no closed form: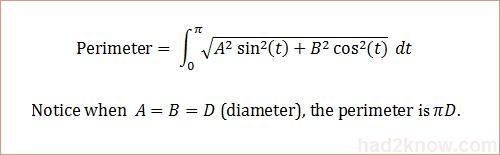

However, there are several approximation formulas that give fairly accurate answers. They are listed in order of decreasing accuracy and decreasing complexity:

Perimeter₁ ≈
(pi/2)(A+B)[1 + H²/4 + H⁴/64 + H⁶/256 + 25H⁸/16384]
where H = |A-B|/(A+B)

Perimeter₂ ≈
(pi/2)(A+B)[1 + 3H²/(10+sqrt(4-3H²))]
where H = |A-B|/(A+B)

Perimeter₃ ≈ (pi/2)[3(A+B) - sqrt(3A² + 10AB + 3B²)]

Perimeter₄ ≈ (pi/2)sqrt(2A² + 2B²)

Example

A swimming pool is in the shape of an ellipse with a width of 12 feet and a length of 17 feet. Find its approximate perimeter and area.

First we set A = 17 and B = 12. Using the area formula, we find that the pool floor has an area of 160.221 square feet.

To find the perimeter, we can use any of the approximation formulas. For this example, we will use the third:

Perimeter ≈ (pi/2)[3(29) - sqrt(432 + 2040 + 867)] = 45.892 feet.

© Had2Know 2010