3 Variable Exponential Regression:
z = ab^xc^y

Using Least Squares Regression to Fit an Exponential Function z = ab^xc^y

The method of multiple linear regression with least squares can be adapted to find curved surfaces that fit a given set of data points in 3-dimensional space. If you model a phenomenon with an exponential function of the form z = ab^xc^y, you can be linear this equation before applying least squares. Observe:

z = ab^xc^y
ln(z) = ln(ab^xc^y)
ln(z) = ln(a) + x*ln(b) + y*ln(c)

This equation is linear in the undetermined coefficients ln(a), ln(b), and ln(c). Following the technique of simple multiple linear regression you can use matrices to calculate ln(a), ln(b), and ln(c).

The matrix equation for this model is


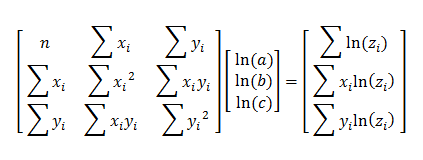
Once you compute the values of ln(a), ln(b), and ln(c), you can use the relation d = e^ln(d) to find a, b, and c.

Example

A researcher hypothesizes that a bacterial colony's growth is an exponential function of time and the nutritive value of the substrate. The size of the colony is measured in square centimeters and denoted by z, the time elapsed is measured in hours and denoted by x, and the food value of the substrate is ranked on a scale from 1 to 10 and denoted by y.

The researcher records the following data:

(1, 1, 0.61)  (1, 3, 0.83)  (1, 7, 1.02)
(1, 1, 0.52)  (1, 3, 0.78)  (1, 7, 1.05)
(2, 1, 1.65)  (2, 3, 2.11)  (2, 7, 2.56)
(2, 1, 1.43)  (2, 3, 2.08)  (2, 7, 2.72)
(3, 1, 2.75)  (3, 3, 4.98)  (3, 7, 5.86)
(3, 1, 2.78)  (3, 3, 4.23)  (3, 7, 5.33)

Using the regression calculator above yields the equation

z = 0.2468(2.3082^x)(1.1011^y)

Using this equation, the researcher can interpolate the size of the colony after 2.5 hours in a substrate that has a nutritive value of 6. Simple plug x = 2.5 and y = 6 into the exponential equation. This gives

z = 0.2468(2.3082^2.5)(1.1011⁶)
= 3.56 cm²

© Had2Know 2010