Golden Ratio Calculator

The golden ratio is so-called because the ancient Greeks found rectangles more aesthetically pleasing when their side lengths were in a ratio of 1:(1 + √5)/2, or approximately 1:1.618034.

The number (1 + √5)/2 is often called the golden section and denoted by φ.

The constant φ appears in a number of algebraic, arithmetic, and geometric relations. For example, the continued fraction

      

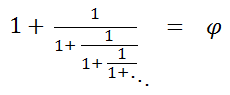
converges to φ. The continued radical

  

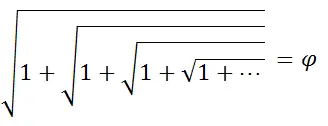
also converges to φ. These two arithmetic expressions can be resolved by solving the algebraic equations

x = 1 + 1/x    and    x = √x+1 .

The only positively valued solution to these two equations is x = φ. (Transform the expressions into quadratic equations and use the quadratic formula.) The golden section is also the limiting ratio of consecutive Fibonacci numbers. For example,

3/2 = 1.5
5/3 = 1.6
8/5 = 1.6
13/8 = 1.625
   ⋮
987/610 = 1.6180323, etc.

To understand φ geometrically, suppose you have a rectangle whose sides are in a ratio of 1:φ. When you cut a perfect square from the rectangle, the remaining rectangle is also a golden rectangle. If you repeat the process over and over, you obtain the pattern shown on the left:
If you want to create a rectangle whose sides are in a ratio of 1:φ, and you know the length of one of the sides, you can quickly compute the length of the missing side with one of the following formulas. Here, "width" denotes the shorter side and "length" denotes the longer side.

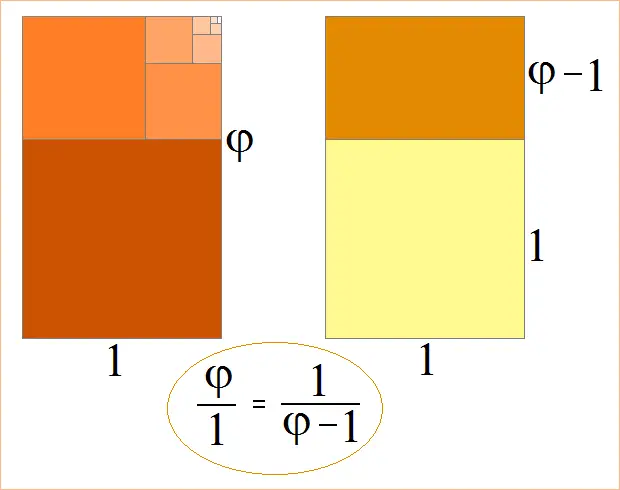
width = length/φ
length = width × φ

© Had2Know 2010