Triangles in the Half-Plane Model of the Hyperbolic Plane

There are several models of the hyperbolic plane, one of which is the upper half-plane model denoted by H.  H is the set of all complex numbers whose imaginary part is positive. In the hyperbolic half-plane, the shortest path between two points is represented by ab arc of a circle whose center lies on the line Im = 0, that is, the lower boundary of the half-plane.

A hyperbolic triangle is a set of three points and the "lines" that join them in the hyperbolic plane. When two points have the same horizontal coordinate, the line that joins them is a vertical line (essentially, an arc of a circle with infinite radius).

Area of a Hyperbolic Triangle

In the hyperbolic half-plane, the area of a triangle is bounded and cannot exceed π. The formula for area is simply π minus the sum of the angles. Since the half-plane model is conformal (preserves angles), you can find each angle of the triangle by computing the intersection angle between circular arcs in radians.

Perimeter of a Hyperbolic Triangle

Distance in the hyperbolic half-plane is defined differently than in Euclidean geometry. If a + bi and c + di represent two points in H, then the distance between a + bi and c + di is given by

cosh^-1[(b² + d² + (a-c)²)/(2bd)]

When a = c, the distance formula simplifies to

|ln(b/d)|

An equivalent formulation of distance can be described in terms of the chord lengths shown in the image below: To find the perimeter of a hyperbolic triangle you simply sum the hyperbolic distances between points. Unlike area, perimeter and distance are unbounded in the hyperbolic half-plane model.

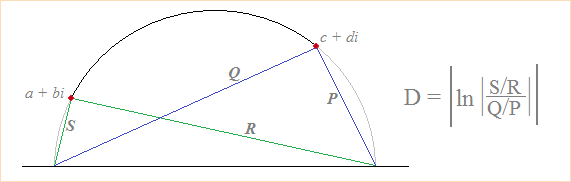
© Had2Know 2010