Ring of n Circles Inscribed Within a Larger Circle

If you create a symmetric ring of n circles in which adjacent circles are tangent, you can circumscribe a larger circle around the ring. Such an arrangement can be used in geometric designs. The mathematical challenge is to find the correct radius of each circle so that there are no gaps or overlapping circles.

The radius of the outer circle depends upon the number n as well as the radius of each circle in the inner ring. Likewise, the radius of each circle in the inner ring circle depends on n and radius of the outer circle.

The formulas for calculating the radii are described below and require only a hand calculator to evaluate. You can also use the calculator on the left. Simply enter the number of circles in the inner ring (n) and the radius of either the outer circle or interior ring circles. The calculator will compute the unknown dimensions of the other circle(s).

See images below for details on how the formulas are derived.

To begin, call the radius of the larger outer circle R, and the radius of the inner ring circles r.

If you connect the centers of two adjacent interior circles and the center of the outer circle, you form an isosceles triangle with sides 2r, R - r, and R - r. The angle θ in the triangle has a measure of 2π/n radians (not degrees). The figure below shows the relations among r, R, and θ. If you know the value of R and n, you can compute r with the equation

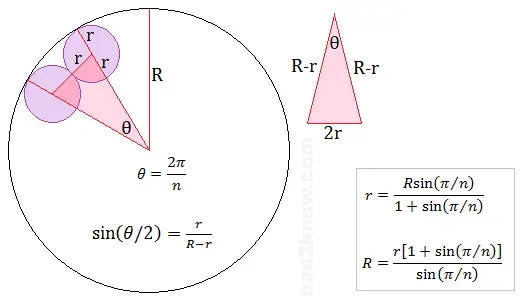
r = Rsin(π/n)/[1 + sin(π/n)].

If you know the value of r and n, you can compute R with the equation

R = r[1 + sin(π/n)]/sin(π/n).

Example: Suppose you make a ring from 12 equal circles, each of which is 6 cm in diameter. Since n = 12 and r = 3 cm, you can compute the radius of the exterior circle with the expression

R = (3)[1 + sin(π/12)/sin(π/12)
= (3)(1.258819)/(0.258819)
= (3)(4.863703)
= 14.59111 cm.

© Had2Know 2010