Integer Triangles with a 60° Angle
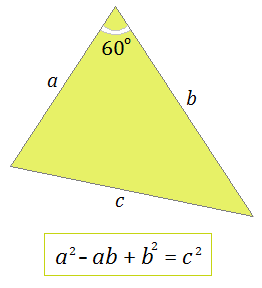
Just as there are integer right triangles, so there are integer 60° triangles. In such triangles, the side lengths are all integers and one of the angles measures exactly 60°.
If a and b denote the two sides which are adjacent to the 60°, and c denotes the remaining side, then a, b, and c satisfy a Pythagorean-like relation:
a² - ab + b² = c².
This relation holds for all 60° triangles, not just those with integer sides.
To find triples (a, b, c) that satisfy the relation a² - ab + b² = c², you can use generator functions similar to the generator functions for Pythagorean triples and 120° triangles, or you can use a trick based on knowledge of 120° triangles. To produce 60° triangles with generator functions, the equations are
a = m² - n²
b = 2mn - n²
c = m² - mn + n²,
where m and n are integers and m > n. This works because
(m² - n²)² - (m² - n²)(2mn - n²) + (2mn - n²)² = (m² - mn + n²)²
How to Generate 60° Triangles With 120° Triangles
Suppose the triple (x, y, z) represents an integer 120° triangle, i.e., x² + xy + y² = z². Then the triples (x+y, y, z) and (x, x+y, z) represent two integer 60° triangles. To confirm this algebraically, start with the known relation x² + xy + y² = z². Rewrite the left hand side in an equivalent form and simplify:x² + xy + y² = z²
x² - x² + x² + xy - xy + xy + y² = z²
x² + 2xy + y² - x² - xy + x² = z²
(x+y)² - (x+y)x + x² = z²
This shows that (x, x+y, z) is an integer 60° triangle. A similar argument shows that (x+y, y, z) is as well. For visual proof, see the animated image below:
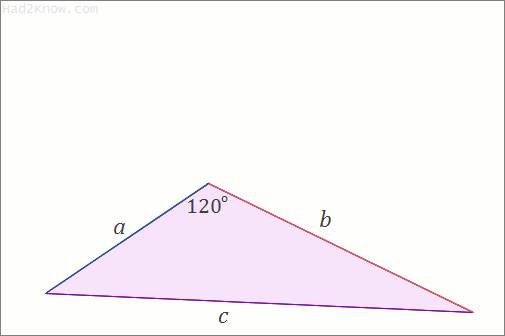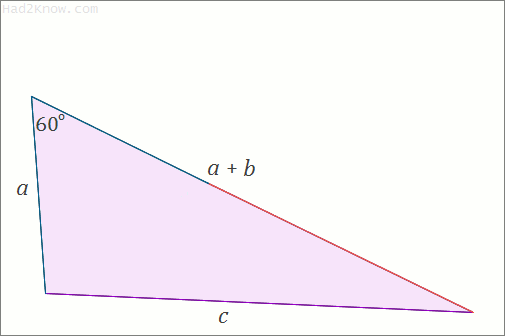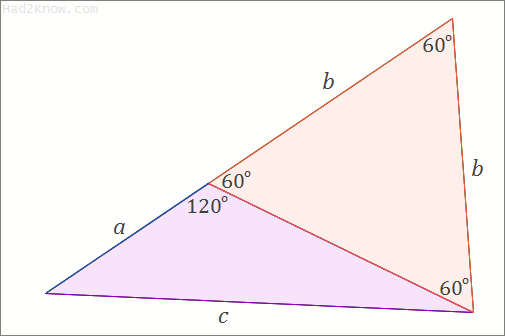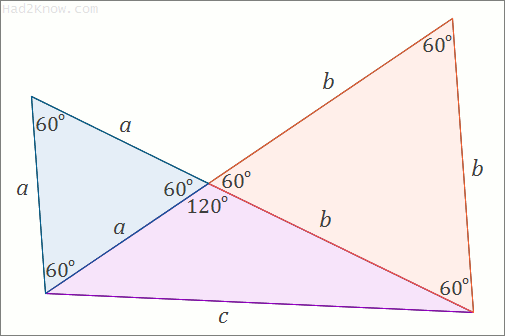
You can use this trick to generate every primitive integer 60° triangle from every primitive integer 120° triangle. The table below shows the first few primitive triples (a, b, c) where c < 100.
| a | b | c |
| 3 | 8 | 7 |
| 5 | 8 | 7 |
| 7 | 15 | 13 |
| 8 | 15 | 13 |
| 5 | 21 | 19 |
| 16 | 21 | 19 |
| 11 | 35 | 31 |
| 24 | 35 | 31 |
| 7 | 40 | 37 |
| 33 | 40 | 37 |
| 13 | 48 | 43 |
| 35 | 48 | 43 |
| 16 | 55 | 49 |
| 39 | 55 | 49 |
| 9 | 65 | 61 |
| 56 | 65 | 61 |
| 32 | 77 | 67 |
| 45 | 77 | 67 |
| 17 | 80 | 73 |
| 63 | 80 | 73 |
| 40 | 91 | 79 |
| 51 | 91 | 79 |
| 11 | 96 | 91 |
| 85 | 96 | 91 |
| 19 | 99 | 91 |
| 80 | 99 | 91 |
| 55 | 112 | 97 |
| 57 | 112 | 97 |
© Had2Know 2010
