How to Find the Intersection Angle of Two Circles

Just as you can compute the angle of intersection between two straight lines, you can also find the intersection angle where two curves cross.

To find the angle, you first use calculus to find the equations of the tangent lines at the intersection point, then compute the angle between the tangent lines However, if both curves are circles, you can use the geometric properties of circles to find the tangents instead of calculus. Or use the calculator on the left. All you need to know is the radius of each circle and the distance between the centers of the circles.

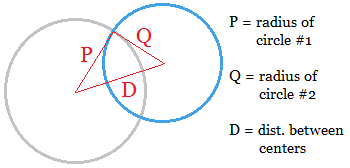
In the image above, the radius of one circle is labeled P and the radius of the other is labeled Q. The distance between the centers is D. You can form a triangle that connects one point of intersection with the two centers.

The angle formed by the two radii is the supplementary angle of the intersection angle. In other words, once you determine the angle θ formed by the radii, then the angle of intersection is φ = 180° - θ.

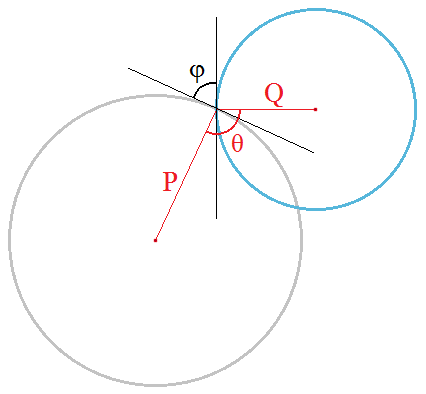
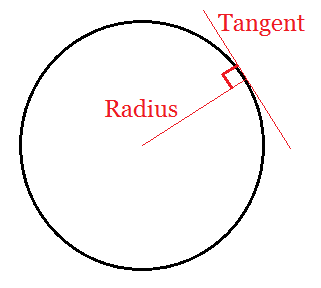
The reason why the angle of the triangle and the angle of intersection add up to 180° is because the angle formed by a radius and its corresponding tangent line is always 90°. And so 90° + 90° + φ + θ = 360°.

Intersection Angle Formula

The angle of the triangle is given by the formula

θ = sin^-1[ sqrt(2P²Q² + 2P²D² + 2Q²D² - P⁴ - Q⁴ - D⁴)/(2PQ) ]

and the angle of intersection by the formula

φ = 180° - θ

Example:
One circle has a radius of 10 and another has a radius of 20. They intersect in such a way that the distance between their centers is 25. What is the angle of intersection?

Set P = 10, Q = 20, and D = 25. (It doesn't matter which radius is labeled P or Q.). Plugging these values into the formula gives you

θ = sin^-1[ √ 80000 + 125000 + 500000 - 10000 - 160000 - 390625  / 400 ]
= sin^-1[ √ 144375  / 400 ]
= sin^-1[ 379.967/400 ]
= 71.79°

Therefore, φ = 108.21°

© Had2Know 2010