Lambert W Function Calculator

The Lambert W function W(x) is defined by the relation

x = W(x)e^W(x).

In other words, the Lambert function is the inverse of the function

f(x) = xe^x,

so W(x) = f^-1(x).

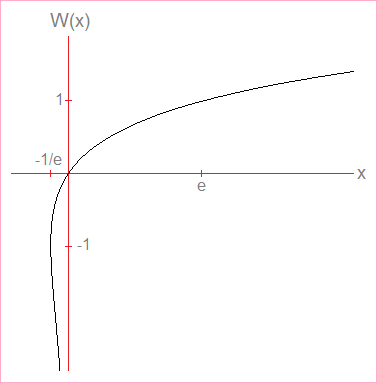
The domain of the Lambert W function is [-1/e, ∞) and the range is (-∞, ∞). However, when x is in the interval (-1/e, 0), the function returns two values of W(x), so the complete Lambert function is not a true function in the strictest sense.

To make the Lambert W function a true function, mathematicians split it into two branches, both of which are one-to-one. W₀(x) denotes the upper part of the Lambert function whose domain is [-1/e, ∞) and range [-1, ∞). W_-1(x) denotes the lower part of the Lambert function whose domain is (-1/e, 0) and range (-∞, -1).

Evaluating W(x)

Because the inverse of the function f(x) = xe^x cannot be expressed in terms of elementary functions, analysts use numerical algorithms to evaluate the Lambert W function at a value of x. The calculator above computes W(X) for any x value in the interval [-1/e, ∞). If x is within the sub interval (-1/e, 0), the calculator returns two values. In this case, the greater value is W₀(x) and the lesser value is W_-1(x).

Some particular values of W(x) are:

W(-1/e) = -1
W(0) = 0
W(e) = 1
W(2e²) = 2

Special Properties of W(x)

The Lambert W function satisfies the functional relations

W(x) = xe^-W(x) and
e^W(x) = x/W(x).

Using the technique of implicit differentiation, you can find the first and second derivatives of W(x), which are

W'(x) = W(x)/[x + xW(x)]
W"(x) = -[2W(x)² + W(x)³]/[x²(1 + W(x))³].

Using the substitution x = ze^z, w(x) = z, and dx = (ze^z + e^z)dz, you can evaluate integrals involving W(x):

∫W(x) dx = xW(x) - x + x/W(x) + C
∫W(x)/x dx = 0.5W(x)² + W(x) + C
∫x/W(x) dx = x²[1/(2W(x)) + 1/(4W(x)²)] + C

Uses of W(x)

The Lambert function arises in many physics and engineering applications. From a mathematical standpoint, the W function can be used to express the solution(s) of other inversion problems.

For example, consider the function A(x) defined by the relation x = 2A(x) + LN[A(x)]. (A(x) is the inverse of the function f(x) = 2x + LN(x).) With the following steps, we can express A(x) in terms of W(x):

x = 2A(x) + LN[A(x)]
e^x = A(x)e^2A(x)
2e^x = 2A(x)e^2A(x)
which implies that
2A(x) = W(2e^x)
A(x) = 0.5W(2e^x)

Here are four more examples with the functions
B(x) defined by x = B(x)²e^B(x),
C(x) defined by x = C(x)LN[C(x)] + 3,
D(x) defined by x = D(x) + 2^D(x),
E(x) defined by x = E(x)^E(x)

* * * * * * * * * *

x = B(x)²e^B(x)
x^0.5 = B(x)e^0.5B(x)
0.5x^0.5 = 0.5B(x)e^0.5B(x)
which implies that
0.5B(x) = W(0.5x^0.5)
B(x) = 2W(0.5x^0.5)

x = C(x)LN[C(x)] + 3
x-3 = C(x)LN[C(x)]
x-3 = e^LN[C(x)]LN[C(x)]
which implies that
LN[C(x)] = W(x-3)
C(x) = e^W(x-3)

x = D(x) + 2^D(x)
2^x = 2^D(x)2^2D(x)
2^x = 2^D(x)e^LN(2)*2D(x)
LN(2)*2^x = LN(2)*2^D(x)e^LN(2)*2D(x)
which implies that
LN(2)*2^D(x) = W(LN(2)*2^x)
2^D(x) = W(LN(2)*2^x)/LN(2)
D(x) = log₂[W(LN(2)*2^x)/LN(2)]

x = E(x)^E(x)
LN(x) = E(x)LN[E(x)]
LN(x) = e^LN[E(x)]LN[E(x)]
which implies that
LN[E(x)] = W(LN(x))
E(x) = e^W(LN(x))

© Had2Know 2010