Lamé Curve Calculator

Lamé curves are generalizations of ellipses. The equation of an ellipse in Cartesian coordinates is

(x/a)² + (y/b)² = 1,

where a and b are the half-width and half-length of the ellipse. The equation of a Lamé curve is

|x/a|ⁿ + |y/b|ⁿ = 1,

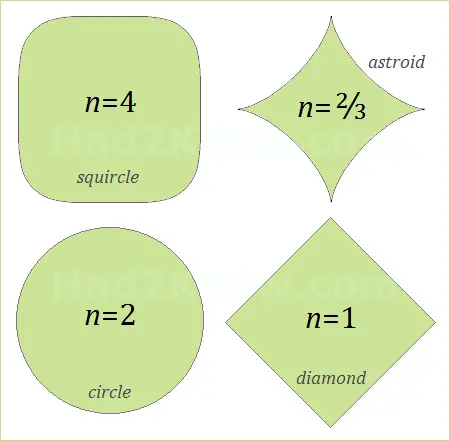
where n is greater than zero. As with the ellipse, a and b are the half-width and half-length, while the third parameter n governs the general shape of the curve. Ellipses and circles are special cases of Lamé curves where n = 2.

Lamé curves in which n is greater than 2 have the eye-pleasing shape of rectangles with rounded corners and are frequently used in design. Sometimes these curves are called superellipses. The city square Sergels Torg in Stockholm, Sweden was constructed in the shape of a superellipse with a = 5, b = 6, and n = 2.5.

When n is between 1 and 2, the curve resembles a diamond with rounded corners and sides that puff outward. In the image below are examples of Lamé curves with different values of a, b, and n. The larger the value of n, the more rectangular the figure becomes.

Some Lamé curves have special names. For example, when n = 4 and a = b, the figure is called a squircle, a portmanteau of square and circle. The figure resembles are square with rounded corners. When n = 2/3 and a = b, the figure is called an astroid (not to be confused with asteroid).

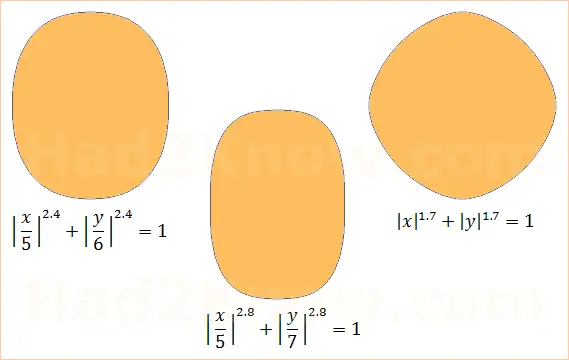
Area of a Lamé Curve

The area of a Lamé curve can be expressed in terms of the Gamma Function. The formula is

Area = 4abΓ(1 + ¹/_n)²/Γ(1 + ²/_n).

There is no similarly neat formula for the perimeter of a Lamé curve, so numerical methods must be employed. You can also use the calculator above to compute the area and perimeter of a Lamé curve. The calculator is most accurate when n is less than 10.

© Had2Know 2010