Laplace Distribution Random Number Generator

The Laplace distribution is a symmetric distribution formed by splicing two exponential distributions. The result is a probability function with a sharp peak and tails that taper off at an exponential rate. One application of the Laplace distribution is in Brownian motion evaluated at time intervals that are exponentially distributed.

To generate random variables with a Laplacian distribution use the calculator below and see figure below for explanation of the parameters a and b

a =       b =       N =
Decimal Precision integer tenths hundredths thousandths	Display comma separated vertical

The probability distribution function for Laplace random variables is shown below. The parameter a gives the center of the distribution, while b is a scaling factor.


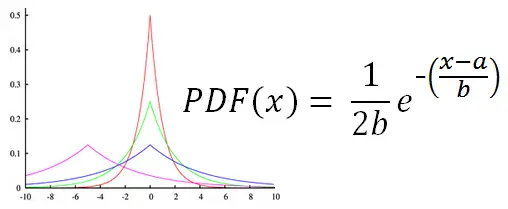
The mean, median, mode, variance, and skewness of the Laplace distribution are easy to calculate for the parameters a and b:

mean = a
median = a
mode = a
variance = 2b²
skew = 0

The Laplace distribution arises in the study of other continuous probability distributions. For instance, if W and Z are random variables drawn from the uniform distribution U(0,1), then the new random variable defined as Ln(W/Z) has a Laplace distribution with parameters a = 0 and b = 1.

Another example: Suppose Y₁, Y₂, Y₃, and Y₄ are independent and identically distributed random variables drawn from a normal distribution with a mean of 0 and variance of 1. Then the new random variables Y₁Y₂ + Y₃Y₄ and Y₁Y₂ - Y₃Y₄ have a Laplace distribution with parameters a = 0 and b = 1.

© Had2Know 2010