Log-Normal Random Number Generator

The log-normal distribution is used to model situations in which the logarithm of a set of numbers fits a normal distribution. Although the parameters μ and σ appear in the PDF of the log-normal distribution, these are not the mean and standard deviation as they are in the normal distribution.

You can use the calculator below to generate a set of log-normally distributed random variables given values of μ and σ. The theoretical mean and variance are described below.

μ =       σ =       N =
Decimal Precision integer tenths hundredths thousandths	Display comma separated vertical

The probability density function of the log-normal distribution is
The mean, median, mode, variance, and skewness of the log-normal distribution are

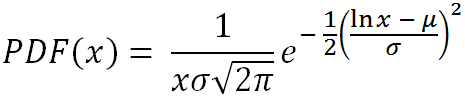
mean = e^(μ + σ²/2)
median = e^(μ)
mode = e^(μ - σ²)
variance = [e^(σ²) - 1]e^(2μ + σ²)
skew = [e^(σ²) + 2]sqrt[e^(σ²) - 1]

© Had2Know 2010