Folding a Cone of Maximal Volume from a Circle

A cone is formed by folding a circular sector so that the two radii meet. For a given circle, you can form cones of many sizes simply by varying the angle size of the sector you cut from the circle. If you cut just a tiny sliver from the circle and connect the edges of the remaining piece, you will end up with a wide, flat cone. If you make a cone from a sector that has a small angle measure, you will end up with a tall, skinny cone.

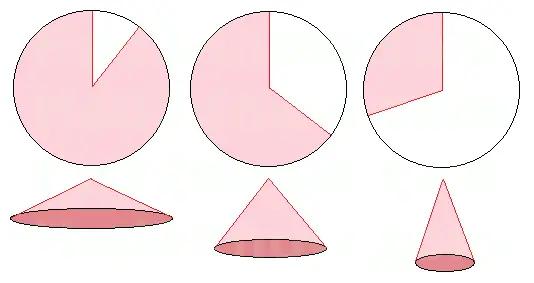
Using calculus, it is possible to determine the sector angle size that will yield a cone of maximum volume. First, if we denote the radius of the circle by R and the angle of the sector by θ (in radians), then the arc length of the sector is Rθ. This is also the circumference of the base of the cone.

If we denote the radius of the cone's base by B and the cone's height by H, then we have

B = Rθ/(2π)
H = R*sqrt(1 - θ²/(4π²))

The volume of the cone, V, is given by the function

V(B,H) = (π/3)B²H                                   or
V(R,θ) = (1/(12π))R³θ²sqrt(1 - θ²/(4π²))

Given a fixed value of R, the angle θ that maximizes the volume must satisfy the equation ∂V/∂θ = 0.

∂V/∂θ = [R³/(12π)]*[1/sqrt(1 - θ²/(4π²))]*[2θ - 3θ³/(4π²)]

Setting this equation equal to zero and solving for θ amounts to solving

2θ - 3θ³/(4π²) = 0.

And so
2 - 3θ²/(4π²) = 0
2 = 3θ²/(4π²)
8π²/3 = θ²
θ = sqrt(8/3)π radians, or 293.94°

Since 360° - 293.94° = 66.06°, you will obtain the cone of maximal volume by removing a sector with an angle of 66.06° and joining the ends of the remaining sector together.

© Had2Know 2010