How to Find the Directrix, Focus, and Vertex of a Parabola

Associated to every parabola is a point inside the curve called the focus and a line outside the curve called the directrix. The focus and directrix are special because every point on the parabola is equidistant from the focus and directrix. In particular, the vertex of the parabola is halfway between the focus and directrix.

The focus lies along the line of symmetry of the parabola, and the directrix is perpendicular to this line. Given the standard equation of a parabola, you can find the coordinates of the focus and vertex, and the equation of the directrix.

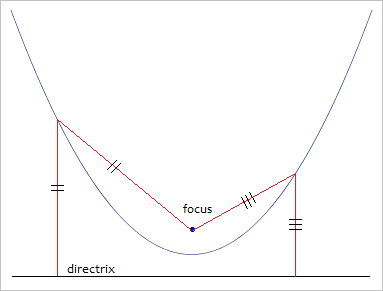
The figure below shows a parabolic arc, its focus, and its directrix. The red lines show that any point on the curve of the parabola has the same distance from the focus as from the directrix

Finding the Vertex

If the equation of the parabola is y = ax² + bx + c, then the x-coordinate of the vertex can by found by solving y' = 0. The derivative is y' = 2ax + b, and so

2ax + b = 0
2ax = -b
x = -b/(2a).

The y-coordinate of the vertex can be found by plugging x = -b/(2a) into the equation of the parabola. This gives you

y-coord = a[-b/(2a)]² + b[-b/(2a)] + c
= c - b²/(4a).

The full coordinates of the vertex are ( -b/(2a), c - b²/(4a) ).

Finding the Focus

The distance from the focus and vertex depends on the coefficient of x². If the parabola opens upward, the focus is 1/(4|a|) units above the vertex. If the parabola opens downward the focus is 1/(4|a|) units below the vertex. Thus, the x- and y-coordinates of the focus are

( -b/(2a), c - b²/(4a) + 1/(4a) )
= ( -b/(2a), c + (1-b²)/(4a) ).

Finding the Directrix

The directrix is 1/(4|a|) units away from the vertex in the opposite direction as the focus. For a standard parabola, it is a horizontal line defined by the equation

y = c - (1+b²)/(4a).

© Had2Know 2010