How to Find a Parabola's Equation from Its Directrix and Focus

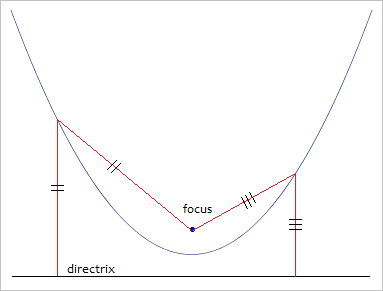
Every parabola has a point inside the curve called the focus and a line outside the curve called the directrix. Each point on the parabola is equidistant from the focus and directrix. If you know the coordinates of the focus and the equation of the directrix, you can use this information to deduce the equation of the parabola.

You can follow the steps below, or use the calculator on the left to find the parabola's equation.

Step 1
Call the focus coordinates (P, Q) and the directrix line Y = R. Given the values of P, Q, and R, we want to find three constants A, H, and K such that the equation of the parabola can be written as

Y = A(X - H)² + K.

The coordinate pair (H, K) is the vertex of the parabola.

Step 2
Since the vertex of the parabola is halfway between the focus and directrix, the x-coordinate of the vertex is P, and the y-coordinate is (Q+R)/2. Thus, we have

H = P
K = (Q+R)/2

Step 3
The inverse of the scaling constant A is 4 times the difference between the height of the focus and the height of the vertex. Mathematically, this can be written as

1/A = 4[Q - (Q+R)/2].

This expression can be simplified to

A = 1/(2Q-2R).

Now that you have the three values of A, H, and K, you can write the equation of the parabola.

Example:
The focus of a parabola is at (3, 6) and the directrix line is Y = 4. What is the equation of the parabola?

First note that you have P = 3, Q = 6, and R = 4. The equations in Step 2 give you

H = 3
K = (6+4)/2 = 5

The equation in Step 3 gives you

A = 1/(12-8) = 0.25

Therefore, the equation of the parabola is

Y = 0.25(X - 3)² + 5

© Had2Know 2010