Padovan/Perrin Sequences and the Plastic Number

The Padovan Sequence and Perrin Sequence are defined by the third-order linear recurrence relation

P(n+3) = P(n+1) + P(n).

The two sequences differ in their initial values. In the Padovan Sequence, P(0) = 1, P(1) = 1, and P(2) = 1. The first several terms of this integer sequence are

1, 1, 1, 2, 2, 3, 4, 5, 7, 9, 12, 16, 21, 28, 37, 49, 65, 86, 114, 151, 200, 265, 351, 465, 616, 816, 1081, 1432, 1897, 2513, 3329, 4410, 5842, 7739, 10252, 13581, 17991, 23833, 31572, 41824, 55405, 73396, 97229, 128801, 170625,...

In the Perrin Sequence, P(0) = 3, P(1) = 0, and P(2) = 2 and the first several terms of this sequence are

3, 0, 2, 3, 2, 5, 5, 7, 10, 12, 17, 22, 29, 39, 51, 68, 90, 119, 158, 209, 277, 367, 486, 644, 853, 1130, 1497, 1983, 2627, 3480, 4610, 6107, 8090, 10717, 14197, 18807, 24914, 33004, 43721, 57918, 76725, 101639, 134643, 178364, 236282, 313007,...

In both sequences, the limiting ratio of consecutive terms is equal to the real root of the characteristic equation x³ - x - 1 = 0. The exact value is

x = ∛ ½ + ⅙⋅sqrt(23/3)  + ∛ ½ - ⅙⋅sqrt(23/3) 

which is approximately equal to

This number is known as the plastic constant or plastic number. Like the Fibonacci Sequence, the n^th term of the Perrin and Padovan Sequences can be calculated explicitly with an exponential sum formula. For the Perrin and Padovan Sequences, the formula is

P(n) = axⁿ + byⁿ + czⁿ,

where x, y, and z are the roots of the equation t³ - t - 1 = 0 and the coefficients a, b, and c depend on the initial conditions P(0), P(1), and P(2).

Properties of the Perrin and Padovan Sequences

Both sequences satisfy the recurrence relations

P(n+5) = P(n+4) + P(n)

P(n+5) = 2 + Σ ⁱ⁼ⁿ _i=0 P(i)

The Padovan Sequence can be visualized by the side lengths of equilateral triangles in a spiral

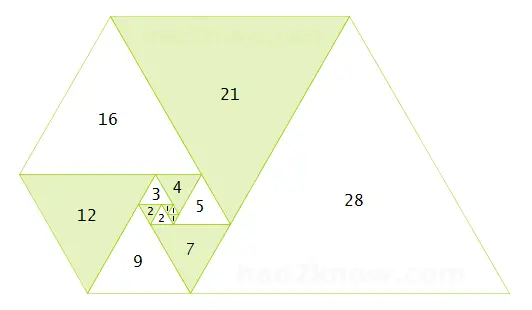
The Perrin Sequence exhibits a remarkable property for prime indices. If q is a prime number, then P_errin(q) is divisible by q. The first several examples of this are

P_errin(2) = 2 = 2⋅1
P_errin(3) = 3 = 3⋅1
P_errin(5) = 5 = 5⋅1
P_errin(7) = 7 = 7⋅1
P_errin(11) = 22 = 11⋅2
P_errin(13) = 39 = 13⋅3
P_errin(17) = 119 = 17⋅7
P_errin(19) = 209 = 19⋅11
P_errin(23) = 664 = 23⋅28
P_errin(29) = 3480 = 29⋅120

The Padovan Sequence figures in some convergent series. If |c| is greater than the plastic constant, then the series

Σ^∞_o P_ad(n)⋅c^-n

converges to c²(c+1)/(c³-c-1). For instance,

Σ^∞_o P_ad(n)⋅2^-n = 12/5

Σ^∞_o P_ad(n)⋅3^-n = 36/23

Values at Negative Indices

Using the initial values of P(0), P(1), and P(2) you can also extend the Padovan and Perrin Sequences to negative integer indices. The first several values of the Padovan sequence from 0 to -50 are

1, 0, 1, 0, 0, 1, -1, 1, 0, -1, 2, -2, 1, 1, -3, 4, -3, 0, 4, -7, 7, -3, -4, 11, -14, 10, 1, -15, 25, -24, 9, 16, -40, 49, -33, -7, 56, -89, 82, -26, -63, 145, -171, 108, 37, -208, 316, -279, 71, 245, -524,...

And for the Perrin Sequence, the first several values from 0 to -50 are

3, -1, 1, 2, -3, 4, -2, -1, 5, -7, 6, -1, -6, 12, -13, 7, 5, -18, 25, -20, 2, 23, -43, 45, -22, -21, 66, -88, 67, -1, -87, 154, -155, 68, 86, -241, 309, -223, -18, 327, -550, 532, -205, -345, 877, -1082, 737, 140, -1222, 1959, -1819,...

© Had2Know 2010