Pythagorean Theorem Proof

The Pythagorean theorem for right triangles, a² + b² = c², was actually already known to the Babylonians before the Pythagoreans decided to investigate the relation. What the Pythagoreans did was provide a solid proof of the fact using a clever argument with areas. Even today, the proof of the Pythagorean theorem is one of the most simple and elegant proofs in geometry.

First consider a right triangle with side lengths a and b and hypotenuse c. At this point, we don't know what the relation among a, b, and c is. The only fact we can extract is that the area of this triangle is ab/2.

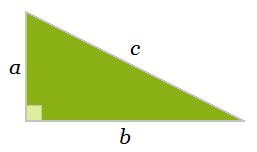
Now take four identical copies of this triangle and arrange them into a large square with a smaller, tilted square inside.



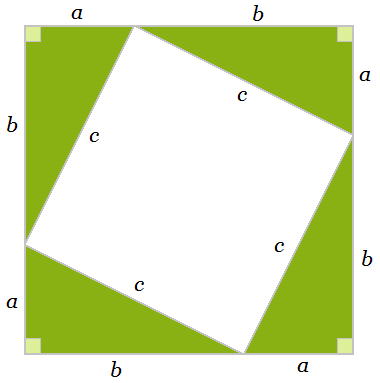
What can we say about the areas of the exterior and interior squares? The side length of the larger square is a + b, so its area is (a + b)². The area of the smaller square can be expressed in two different ways.

Since its side length is c, we can see that its area is c². But its area is also equal to the area of the larger square minus the areas of the four triangles. This is

(a + b)² - 4(ab/2).

Thus we have

c² = (a + b)² - 4(ab/2)
c² = (a² + 2ab + b²) - 2ab
c² = a² + b².

Alternative Proof

You can arrange the four triangles into a square in another way: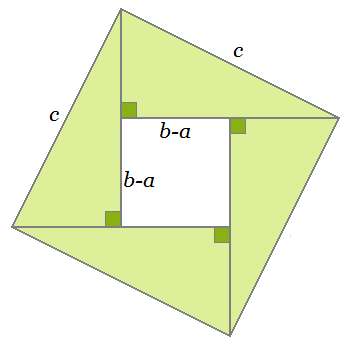



In this figure, the area of the larger square is c². The area of the interior square can be expressed in two different ways.

Since the side length of the smaller square is b - a, its area is (b - a)². But also its area can be expressed as the area of the larger square minus the areas of the four triangles. Thus, we obtain the equality

(b - a)² = c² - 4(ab/2)
b² - 2ab + a² = c² - 2ab
b² + a² = c².

© Had2Know 2010