Pythagorean Triple Calculator

Find All Triangles with a Given Hypotenuse

For every right triangle that has legs of length A and B and a hypotenuse of length C, the relation among A, B, and C is

A² + B² = C², or
sqrt(A² + B²) = C

If A, B, and C are integers then the set (A, B, C) is called a Pythagorean Triple. Some of the most basic examples of Pythagorean Triples are

(3, 4, 5)
(5, 12, 13)
(8, 15, 17)
(7, 24, 25)
(20, 21, 29)

The examples above are called primitive because none of the three terms have a common factor. The set (6, 8, 10) is another Pythagorean Triple, but it is not primitive because you can divide each element by 2, yielding the primitive set (3, 4, 5). Every non-primitive set can be reduced to a primitive set.

There are often many Pythagorean triples that share the same hypotenuse. For example, there are four integer right triangles that have a hypotenuse of 65:

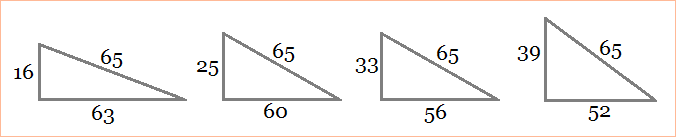
The triples (16, 63, 65) and (33, 56, 65) are primitive, while the triples (25, 60, 65) and (39, 52, 65) are not.

The number of Pythagorean triangles with a given hypotenuse does not depend upon the size of the hypotenuse, but rather on the prime factors of the hypotenuse. To write the formula for the number of Pythagorean triangles with a hypotenuse of N, first decompose N into its prime factors:

N = 2^a₀(p₁^a₁·p₂^a₂···p_k^a_k)(q₁^b₁·q₂^b₂···q_r^b_r)

where the p's are prime factors of the form 4m + 3 and the q's are prime factors of the form 4m + 1. The number of integer right triangles is

[(2b₁ + 1)(2b₂ + 1)···(2b_r + 1) - 1]/2.

For instance, consider the hypotenuse lengths 2465 and 2471. Since 2465 = 5·17·29 and these prime factors are all of the form 4m + 1, there are

[(2·1 + 1)(2·1 + 1)(2·1 + 1) - 1]/2 = (27 - 1)/2 = 13

Pythagorean triangles that have a hypotenuse of 2465. But 2471 = 7·353, and only 353 is of the form 4m + 1. So there is only one integer right triangle with a hypotenuse of 2471.

© Had2Know 2010