Folding a Rectangular Box of Maximal Volume (Open Top)

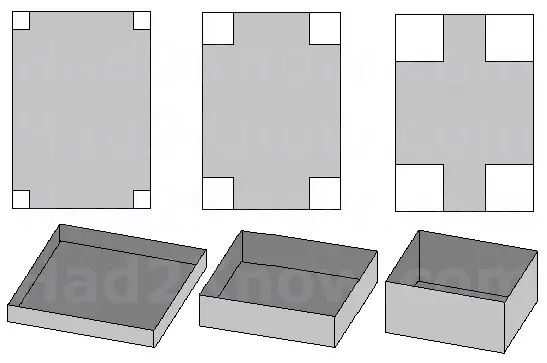
A rectangular box can be formed by cutting out four equal sized squares from the corners of a rectangular sheet of paper, then folding up the flaps and sealing the edges. You can form boxes of many sizes simply by varying the size of the square that you cut from the corners.

If you cut out small squares and connect the edges of the flaps, you obtain a box with a long and wide base and small height. If cut out larger squares, your box will be taller but with a smaller base.

With calculus, you can determine the square size that will result in a box with maximal. This can prove useful if you are making your own storage or shipping containers.

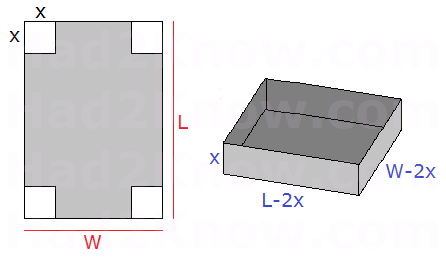
If the width and length of the paper are W and L, and the side length of each corner cut out is X, then the volume of the box is given by the equation

V = X(L-2X)(w-2X)

This is because the volume is equal to the product of a box's length, width, and height. In this case, the box has a length of L-2X, a width of W-2X, and a height of X.

Treating L and W as constants, we will find the optimal value of X when we solve dV/dX = 0:

V = X(L-2X)(w-2X)
V = 4X³ - 2(L+W)X² + (LW)X
dV/dX = 12X² - 4(L+W)X + LW

12X² - 4(L+W)X + LW = 0
X = [4L + 4W ± sqrt(16(L+W)² - 48LW)]/24
X = [4L + 4W ± sqrt(16L² - 16LW + 16W²)]/24
X = [L + W ± sqrt(L² - LW + W²)]/6

Since the squares cannot be larger than the rectangular sheet, the unique solution is
X = [L + W - sqrt(L² - LW + W²)]/6

Example: Suppose a rectangular sheet is 45 by 24. To find the optimal size of square to cut away from the corners, we plug L = 45 and W = 24 into the equation

X = [L + W - sqrt(L² - LW + W²)]/6

which gives us

X = [45 + 24 - sqrt(2025-1080+576)]/6
= [69 - sqrt(1521)]/6
= [69-39]/6
= 5.

This yields a box with dimensions 35 by 14 by 5 having a volume of 2450.

© Had2Know 2010