Volume of a Rectangular Trapezoidal Trough

Trapezoidal rectangular and pyramidal troughs are frequently used in agriculture and heavy industry. Troughs may be either trapezoidal prisms with two sides that are at right angles to the base, or they may be pyramidal with all fours sides slanting toward the base.

If you know the width (W) and length (L) of the top of the trough, the width (a) and length (b) of the trough's base, and the height (H) of the object, then you can calculate its volume with a simple polynomial formula.

The formula for the volume of a trough is derived by breaking up the solid region into simpler pieces. There is a rectangular prism in the center, triangular prisms on the sides, and pyramids at the corners (depending on the shape). Once you compute the volumes of the simpler shapes, you can add them to find the volume of the entire trough.

The volume formula in terms of W, L, a, b, and H is

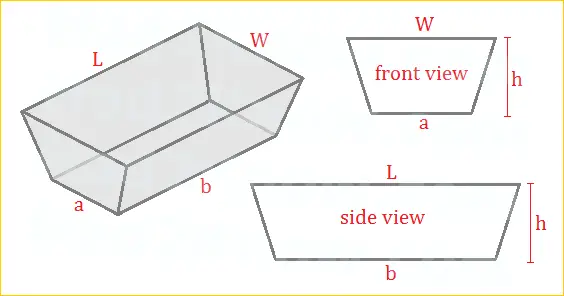
V = H[ab + 0.5(W-a)b + 0.5(L-b)a + (1/3)(W-a)(L-b)]
= (H/6)[6ab + 3Wb - 3ab + 3La - 3ba + 2WL + 2ab - 2Wb - 2aL]
= (H/6)[2WL + Wb + La + 2ab]
= (H/6)[WL + (W+a)(L+b) + ab]

Example: A trough has a base width of 30 cm and a base length of 60 cm. The top of the trough is 40 cm wide and 100 cm long. If the height is 25 cm, what is the volume of the container?

We have a = 30, b = 60, W = 40, L = 100, and H = 25. The volume is thus

V = (25/6)[40*100 + 70*160 + 30*60]
= (25/6)[17000] = 70833.33 cm³.

Notes: When W = a or L = b, the trough is a trapezoidal prism. If W/a = L/b (or equivalently W/L = a/b), the trough is a pyramidal frustum. In the case of a pyramidal frustum the volume formula can be written as

V = (H/3)[WL + sqrt(WLab) + ab].

© Had2Know 2010