How to Solve ab^x = cx + d

Linear functions have the form y = cx + d and exponential functions have the form
y = ab^x, where b is greater than 0. (If b is negative, the domain of the function is rational numbers of the form p/q where q is odd; if b = 0, the function collapses to y = 0.)

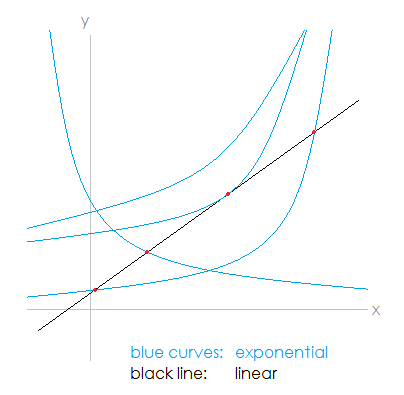
These equations can intersect in several ways. The line can intersect the curve in two distinct points, it can intersect tangentially at one point, it can intersect non-tangentially at one point, or the line may not intersect the curve at all. (See image below.)

To find the points of intersection, you must solve the equation ab^x = cx + d. If c is not equal to 0 and b is a positive number not equal to 1, then the equation cannot be solved algebraically. However, you can use a graphing calculator to approximate the intersection points with a high degree of accuracy, or you can use a numerical recursion algorithm. The equation solving calculator on the left solves for the values of x with accuracy up to 5 decimal places.

One way to simplify the calculations is the divide both sides of the equation by c and thus transform the equation into AB^x + D = x, where A = a/c, B = b, and D = -d/c.

© Had2Know 2010