Spherical Trigonometry Calculator

Jump to Spherical Trigonometry Calculator

A spherical triangle is the region enclosed by three great circular arcs on a sphere. The planes on which these great circle lie intersect at the center of the sphere, creating three angles in the sphere's interior, known as the subtending angles. The dihedral angles of these planes correspond to the angles on the surface of the sphere, known as the spherical angles. Subtending angles are denoted by a, b, and c, while spherical angles are denoted by A, B, and C. Angle a is opposite of angle A, b is opposite of B, and c is opposite of C.

Unlike angles in planar triangles, which must add up to 180°, the angles of a spherical triangle do not always add up to the same number. Thus, there are many non-congruent equilateral spherical triangles and right-angled isosceles spherical triangles.

A spherical triangle's area is (A + B + C - π)r², where r is the radius of the sphere and A, B, and C are measured in radians. If you know 3 of the 6 fundamental angles, you can use spherical trigonometry to solve for the remaining 3 angles, the area of the spherical triangle, the area of the planar triangle formed by the 3 corners of the spherical triangle, as well as the volume of the tetrahedron formed by the 3 corners and the center of the sphere. You can also use the calculator below.

Spherical Trigonometry Calculator
Degrees      Radians
Select the 3 known angles from the options below and fill in their values, plus the value of the radius: 3 spherical angles       A =    B =    C = 2 spherical angles and subtending angle between       A =    B =    c = 2 spherical angles and adjacent subtending angle       A =    B =    a = 3 subtending angles       a =    b =    c = 2 subtending angles and spherical angle between       a =    b =    C = 2 subtending angles and adjacent spherical angle       a =    b =    A =   radius =	Hint: You can type "pi" for expressions in radians as long as you use the * and / symbols for multiplication and division. Example: 3*pi/2 or 1.5*pi are correct entries, but 1.5pi is not.

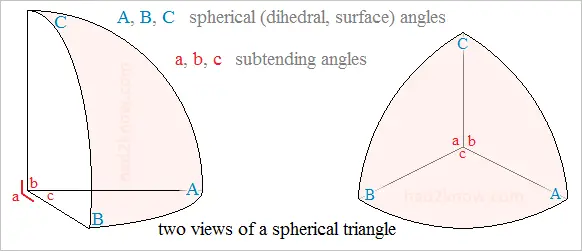
Spherical Trigonometry Formulas

If you know at least three of the 6 angles in a spherical triangle, you can use trigonometric relations to solve for the unknown angles. In the formulas below, A, B, and C are the spherical angles, while a, b, and c are the subtending angles.

© Had2Know 2010