Home » Academics » Square Root of 2 Ratio Calculator

Square Root of 2 Ratio Calculator

Many standard paper sizes are rectangles that have an aspect ratio of 1:√2, or approximately 1:1.41421356. The number √2 is specially chosen because when you cut the rectangle in half parallel to the shorter side, you obtain two smaller rectangles whose aspect ratio is still 1:√2.

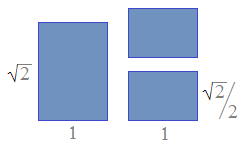
This is because √2/1 = 1/(√2/2), or equivalently √2 = 2/√2. Algebraically, √2 is the unique positive solution to the equation x = 2/x.

For Pythagorean triples in which the legs differ by 1, the square root of two is the limiting ratio of the hypotenuse to the leg length. The ratio of the sum of the legs to the hypotenuse also converges to √2. The first several triples with this property are

(3, 4, 5)
(20, 21, 29)
(119, 120, 169)
(696, 697, 985)
(4059, 4060, 5741)
⋮

Notice that

5741/4059 = 1.41439
5741/4060 = 1.41404
(4060+4059)/5741 = 1.41421355

If you want to create a rectangle whose sides are in a ratio of 1:√2, and you know the length of one of the sides, you can quickly compute the length of the missing side with one of the following formulas. Here, "width" denotes the shorter side and "length" denotes the longer side.

width = length/√2
length = width × √2

Example: The length of a piece of paper is 39 cm. In order for the paper to have an aspect ratio of 1:√2, what should the width be, to the nearest millimeter?

Since the length is 39, the width must be 39/√2, or 27.6 cm (276 mm).

1:√2Aspect Ratio Calculator
Enter Known Dimension: Width A = Length B =
Round to the nearest...