Tetrahedral Volume from Vertex Coordinates

In geometry, tetrahedra are 3-dimensional solids that have 4 vertices, 6 edges, and 4 triangular faces. They are also known as "triangular pyramids;" in their natural orientation they have a triangular base and 3 triangular sides that meet at a point.

If you know the coordinates of the vertices of a tetrahedron, you can compute its volume with a matrix formula.

You can also use the convenient volume calculator on the left. Simply enter the coordinates of four vertices in any order and click the "Find Volume" button.

The Matrix Formula

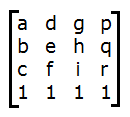
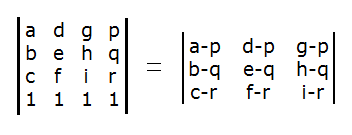
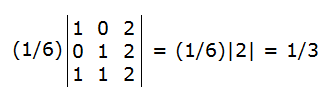
Call the four vertices of the tetrahedron (a, b, c), (d, e, f), (g, h, i), and (p, q, r). Now create a 4-by-4 matrix in which the coordinate triples form the columns of the matrix, with a row of 1's appended at the bottom: The volume of the tetrahedron is 1/6 times the absolute value of the matrix determinant. For any 4-by-4 matrix that has a row of 1's along the bottom, you can compute the determinant with a simplification formula that reduces the problem to a 3-by-3 matrix: Example: A tetrahedron has vertices at (0, 0, 0), (1, 0, 1), (0, 1, 1), and (2, 2, 2). We can use the simplification formula and compute the determinant of a 3-by-3 matrix whose columns are (1, 0, 1), (0, 1, 1), and (2, 2, 2). Dividing this determinant by 6 yields the volume. In this example, the volume of the tetrahedron is 1/3.

© Had2Know 2010