Parabolic Trajectory Calculator

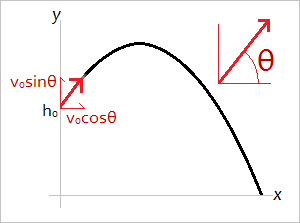
When an object is launched close to the surface of the Earth and the drag force is ignored, the trajectory of the object follows the shape of a parabola. If the initial height of the object is h₀, the initial velocity v₀, and the trajectory angle θ, then the parametric equations of the parabola are

y(t) = h₀ + (sinθ)v₀t - (g/2)t²
x(t) = (cosθ)v₀t,

where y(t) is the y-coordinate of the object at time t, x(t) is the x-coordinate of the object at time t, and g is the gravitational acceleration constant 9.8 m/s². See figure below.

How to Derive These Equations

Since the velocity is a vector, it must be broken down into its x-components and y-components. The velocity in the x-direction is (cosθ)v₀ and the velocity in the y-direction is (sinθ)v₀. The horizontal trajectory of the object maintains constant velocity since there are no other horizontal forces.

The vertical trajectory of the object is subject to deceleration due to gravity, hence the -(g/2)t² term. The reason for dividing g by 2 is so that when you take the second derivative of y(t) you obtain g.

Critical Points

To calculate when the object reaches its maximum height, set y'(t) = 0 and solve for t. If you plug this value into the equation y(t), you can find the maximum height in meters.

To calculate when the object reaches the ground, set y(t) = 0 and solve for t. The larger of the two solutions gives you the time when the object's height is 0. If you plug this value into the equation x(t), you can find how far away the object lands, i.e., its total horizontal displacement.

© Had2Know 2010