Variance and Standard Deviation Calculator

Variance and standard deviation are statistics that measure how spread out a set of data is. If the variance and s.d. of Set A is lower than that of Set B, it means that Set A's data is more clustered around the mean than Set B's.

Since standard deviation is the square root of variance, s.d. is often denoted by σ and variance by σ².

There are two formulas for variance/standard deviation depending on whether the set of numbers represents the entire population being studied, or is just a sample from a much larger population.

The formulas are explained below, but you can also use the convenient variance and standard deviation calculator on the left to compute statistics for large sets of numbers.

Population (Theoretical) Variance

The variance of an entire set is

 σ² = (1/n)Σ(X_i - X)²,

where X_i is a data point, n is the number of points, and X is the arithmetic mean. Population standard deviation is the square root of this expression.

You should use this formula when you can obtain data from every individual in the study group. For example, computing the standard deviation of final grades in a particular class, or finding the variance in property tax rates in a small town where the records are complete.

However, if your data set is only a sample from a much larger population, you must use the estimated variance formula. This is often denoted by 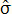²; the caret indicates an estimator statistic.

Sample (Estimated) Variance

The formula for estimated variance is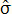

² = [1/(n-1)]Σ(X_i - X)².

The sample s.d. is simply the square root of this expression. The only difference between the population variance and sample variance equations is the first coefficient. In estimated variance, if the sample size is n, then you multiply the summation by 1/(n-1) rather than 1/n.

Use the estimated variance formula when the study population is too large. For example, if you want to estimate the variance in shoe size among women in a large city, you would first select a random sample of n women, and then calculate their shoe size variance using the second formula.

© Had2Know 2010