How to Write a Parabolic Equation in Vertex Form

In algebra, there are three ways to write the equation of a parabola (2^nd degree polynomial) in Cartesian coordinates. The standard form of a parabola is

y = f(x) = ax² + bx + c.

The factored form is

y = f(x) = a(x - r)(x - s),

where r and s are the roots of the function, possibly complex numbers. The vertex form of a parabola is

y = f(x) = a(x - h)² + k,

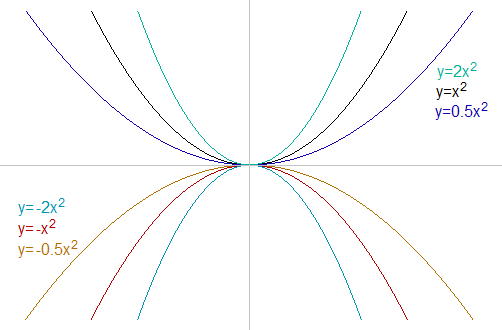
where h is the x-coordinate of vertex and k is the y-coordinate. In all three forms, the coefficient a governs the shape of the parabola. When a is positive, the curve is concave up, and when a is negative the curve is concave down. If a = 0 the function f(x) is a line. See figure below:

How to Convert from Standard Form to Vertex Form

The standard form is the most compact way to write the three terms of a second degree polynomial. However, if you need to draw the graph of a parabola, the vertex form is more convenient. The vertex is located at the point (h, k) and the parameter a indicates the general shape of the parabola. Once you have the equation in the form f(x) = a(x - h)² + k, you have all the information you need to draw the curve.

You can convert the standard form of a parabola to vertex form by completing the square. Doing this yields the relation:

ax² + bx + c   =    a(x + ^b/_2a)² + c - ^b²/_4a .

So h = - ^b/_2a and k = c - ^b²/_4a . You can also use the converter calculator above to quickly transform a parabolic equation into vertex form.

Example: Convert the parabola f(x) = 5x² - 20x + 1 to vertex form. Solution: Since we have a = 5, b = 20, and c = 1, we plug these values into the equivalence relation above. This gives us

5x² - 20x + 1 = 5(x - 20/(2*5))² + 1 - (20²)/(4*5)
= 5(x - 2)² - 19

This means the vertex of the parabola is at the point (2, -19) and the parabola is concave up.

© Had2Know 2010