How to Calculate the Diameter of a Circular Bolt Pattern

Bolts arranged in a circular or regular polygon pattern offer the most stability and strength for wheels and other mechanical parts. Bolt circle patterns usually have 3 to 8 bolts spaced equally along the circumference of a circle, forming an equilateral triangle, square, regular pentagon, hexagon, heptagon, or octagon.

If you have a set of bolts arranged in a circular pattern, but you don't know the diameter of the circle, you can figure the diameter using high school geometry and trigonometry. Three easy methods are explained below. You can also use the calculator on the left. Just enter the number of bolts and the distance between two adjacent bolts.

Method 1 (Even Number of Bolts Only)

If you have an even number of bolts arranged as a regular polygon, the diameter of the circle is simply the distance between opposite bolts. For example, if you have four bolts arranged as a square, the diameter of the circle is the diagonal of the square. If you have six bolts placed in a hexagon pattern, the diameter of bolt circle is equal to the distance between opposite corners.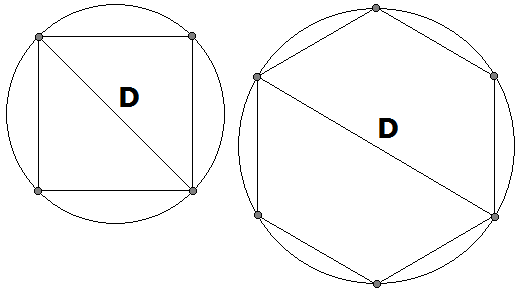

Method 2: Distance Between Neighboring Bolts (Even or Odd)

This method is ideal if you have an odd number of bolts. When you have an odd number of bolts, there is no bolt directly across from another. However, if you know the distance between two adjacent bolts, you can use a trigonometric formula to find the diameter of the circle that the bolts lie on.

Diameter = P/sin(180/n),

where P is the distance between neighboring bolts (measured center to center), and n is the number of bolts. When computing sin(180/n), be sure to set your calculator to degree mode, rather than radians. Or just use the calculator above.

Method 3: Distance Between Semi-Opposite Bolts (Odd Number of Bolts Only)

For an odd number of bolts, you can figure the diameter of the circle using the distance between semi-opposite bolts--two bolts that are as far as possible, but not quite opposite.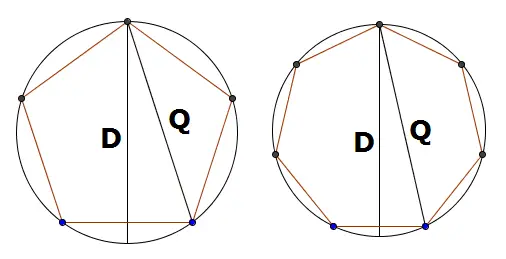



If the semi-opposite distance is Q, then the diameter is given by the equation

Diameter = Q/cos(90/n),

where n is the number of bolts and cosine is measured in degrees, not radians. For example, if you have seven bolts arranged in the shape of a regular heptagon, and the distance between semi-opposite bolts is 23 cm, then the diameter of the circle is

23/cos(90/7)
= 23/cos(12.86)
= 23/0.9749
= 23.59 cm

© Had2Know 2010