How to Calculate Sum-of-Years Depreciation
Sum-of-years, (aka SOY or sum of the years' digits) is a method of figuring asset depreciation. Like double declining balance depreciation, it is a method of accelerated depreciation that assumes an object loses more of its value in the early part of its useful life. It predicts more rapid decrease in value than straight line depreciation, but less rapid than double declining balance or exponential depreciation.
To compute the sum-of-years depreciation, you must first compute the sum of the years in the lifespan of the object, and then use that number to compute the percent decrease for each year. The example below will show you how to calculate the asset's diminished value at the end of each year. Or, you can use the calculator on the left to find an explicit formula for the object's worth.
Sum of the Years' Digits Method
If the useful life of the object is L years, then first compute the sum of the all the numbers between 1 and L. For example, if a server lasts 8 years, then the sum of the years is1+2+3+4+5+6+7+8 = 36.
Next, compute the total loss of value over the lifespan of the object. For example, if the server costs $6000 and its scrap value is $600, then the total loss is $6000 - $600 = $5400. Now determine each years' depreciation using the following pattern:
| Year 1 | Loss = (8/36)(5400) = $1200 |
| Year 2 | Loss = (7/36)(5400) = $1050 |
| Year 3 | Loss = (6/36)(5400) = $900 |
| Year 4 | Loss = (5/36)(5400) = $750 |
| Year 5 | Loss = (4/36)(5400) = $600 |
| Year 6 | Loss = (3/36)(5400) = $450 |
| Year 7 | Loss = (2/36)(5400) = $300 |
| Year 8 | Loss = (1/36)(5400) = $150 |
For this method, you take the year divided by the sum of the years (in reverse order) to determine the ratio of loss for each year. Putting it all together, the value at the end of each year is
| Year 1 | End of Year Value = 6000 - 1200 = $4800 |
| Year 2 | End of Year Value = 4800 - 1050 = $3750 |
| Year 3 | End of Year Value = 3750 - 900 = $2850 |
| Year 4 | End of Year Value = 2850 - 750 = $2100 |
| Year 5 | End of Year Value = 2100 - 600 = $1500 |
| Year 6 | End of Year Value = 1500 - 450 = $1050 |
| Year 7 | End of Year Value = 1050 - 300 = $750 |
| Year 8 | End of Year Value = 750 - 150 = $600 |
You can also find an explicit equation V(t) for the value at the end of year t. Call C the original price, S the scrap value, and L the lifespan. Then the equation is
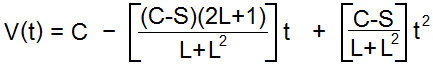
Using the example above, the value equation for the server is
V(t) = 6000 - 1275t + 75t2.
© Had2Know 2010
