Copyright © Had2Know 2010-2025. All Rights Reserved.
Terms of Use | Privacy Policy | Contact
Site Design by E. Emerson
Play Rock-Paper-Scissors-Spock-Lizard Online
Rock-paper-scissors-Spock-lizard is a five-gesture extension of the classic three-gesture roshambo game. RPSSL adds two additional moves, Spock and lizard. The rules are:
Rock crushes scissors and lizard
Paper covers rock and disproves Spock
Lizard eats paper and poisons Spock
Scissors cuts paper and decapitates lizard
Spock crushes scissors and vaporizes rock.
See the history of the game and mathematical trivia below the RPSSL simulator.
About Rock-Paper-Scissors-Spock-Lizard
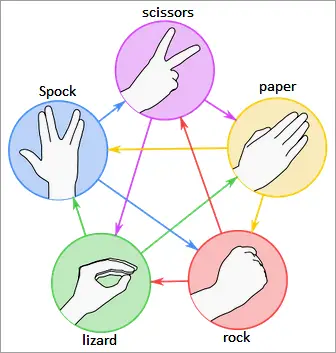
Rock-paper-scissors-Spock-lizard was invented by Sam Kass and Karen Bryla in the mid-'90s as a way to reduce the frequency of ties in roshambo. In a random three-gesture game, the probability of a tie is 1/3, and if two players know each other's habits well enough, the chances of a tie are higher.
In RPSSL, each gesture beats two gestures and is beaten by the remaining two gestures, thus, none of the five symbols has an advantage over the others. The probability of two players making the same move in a random game is only 1/5 (20%). On average, in a series of random rounds, the probability that Player A wins is 2/5 (40%), and that of Player B is 2/5 (40%). This is shown in the table of outcomes below.
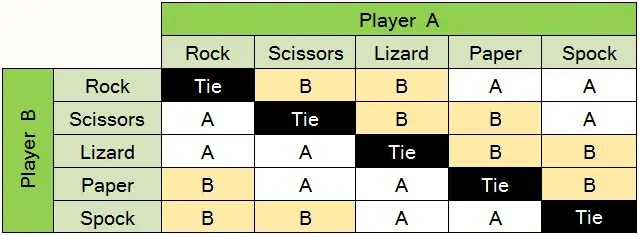
In RPSSL, each gesture beats two gestures and is beaten by the remaining two gestures, thus, none of the five symbols has an advantage over the others. The probability of two players making the same move in a random game is only 1/5 (20%). On average, in a series of random rounds, the probability that Player A wins is 2/5 (40%), and that of Player B is 2/5 (40%). This is shown in the table of outcomes below.

How to Form Spock and Lizard
To make the lizard gesture, fold your hand as though you were making the mouth of a sock puppet. To make the Vulcan salute of Spock, form your fingers into "V" with your thumb, index finger, and middle finger on one side, and your ring finger and pinky on the other. Most people need to practice moving their ring finger independently in order to form the Spock gesture quickly.
About the Pentagram Diagram
Excluding rotations and reflections, there are only two distinct ways to arrange the five symbols of rock-paper-scissors-Spock-lizard into the five corners of the pentagram flow chart:
Rock → Scissors → Lizard → Paper → Spock → Rock → ...
Rock → Lizard → Spock → Scissors → Paper → Rock → ...
Rock → Scissors → Lizard → Paper → Spock → Rock → ...
Rock → Lizard → Spock → Scissors → Paper → Rock → ...
Trinomial Probability Distribution for Wins and Ties
The number of times that A wins, B wins, and A and B tie is distributed according to the trinomial distribution with probabilities 0.4, 0.4, and 0.2. In a game of n rounds, the probability that A will win a times, B will win b times, and A and B will tie t times is given by the expression
P(a, b, t) = [n!/(a!b!t!)](0.4)a(0.4)b(0.2)t
Examples: In a game of 5 rounds, the probability that A wins twice, B wins twice, and once tie is
[5!/(2!2!1!)](0.4)²(0.4)²(0.2) = 480/3125 = 0.1536
In a game of 10 rounds, the probability that A wins 4 times, B wins 4 times, and twice tie is
[10!/(4!4!2!)](0.4)⁴(0.4)⁴(0.2)² = 32256/390625 = 0.08257536
P(a, b, t) = [n!/(a!b!t!)](0.4)a(0.4)b(0.2)t
Examples: In a game of 5 rounds, the probability that A wins twice, B wins twice, and once tie is
[5!/(2!2!1!)](0.4)²(0.4)²(0.2) = 480/3125 = 0.1536
In a game of 10 rounds, the probability that A wins 4 times, B wins 4 times, and twice tie is
[10!/(4!4!2!)](0.4)⁴(0.4)⁴(0.2)² = 32256/390625 = 0.08257536
Other Expansions of Roshambo
For every odd number you can create an expansion of the classic rock-paper-scissors game in which each gesture beats and is beaten by an equal number of other gestures. The more moves you add, the lower the incidence of ties. For example, in a seven-gesture game, the chance of a tie is 1/7 (14.29%). In a 25-gesture game, the probability of a tie is only 1/25 (4%).
Of course, the challenge in developing and playing such games is inventing enough distinct gestures, remembering them, and remembering the other gestures they beat. One enthusiast has created a rock-paper-scissors game of 101 gestures, most of which require two hands to form.
Of course, the challenge in developing and playing such games is inventing enough distinct gestures, remembering them, and remembering the other gestures they beat. One enthusiast has created a rock-paper-scissors game of 101 gestures, most of which require two hands to form.
© Had2Know 2010
