How to Calculate Graduated Payment Mortgages

Graduated Payment Calculator and Formula

A Graduated Payment Mortgage, GPM, is an alternative payment plan that benefits first time borrowers who may earn more money as time passes. In a GPM, the monthly payments start out at a lower rate, and gradually increase every year for 2-5 years until they level off.

For example, suppose you have a graduated mortgage with an initial monthly payment of $640, 2 annual "graduations," and a 5% growth rate between graduations. Then the first year you would pay $640 per month, the second year you would pay $672 a month, and from the third year and beyond you would pay $705.60 each month. This can be beneficial if you expect your income to increase in later years.

You can use the GPM calculator on the left to compute the initial and subsequent payments if you know the mortgage terms. Below we discuss the formula for graduated payment mortgages, so you can also plug the loan variables into the equation and compute your payments by hand.

Variables:

• M = number of years in loan period
• i = annual interest rate, expressed as a decimal (for calculator, leave as percent) Example: 12% = 0.12
• P = principal, the amount borrowed
• N = number of graduations, usually between 2 and 5
• g = graduated growth rate, expressed as a decimal (for calculator, leave as percent) Example: 7% = 0.07

The formula for the monthly payment amount in the first year is

To find the monthly payments in the 2nd year, just multiply the initial year's payment by a factor of (1+g). To figure the monthly payment in the 3rd year, multiply the 2nd year's payment by (1+g) again, and so on. Here is an example computation to illustrate how GPM works:

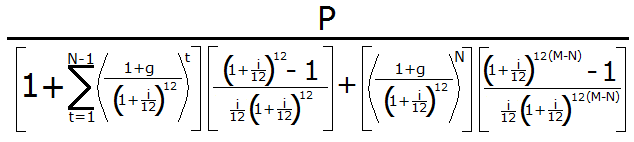
Suppose you take out a loan for $100,000 for 30 years at an annual rate of 8.4%. The graduated payments increase for the first 5 years before they level off, and the rate of increase is 6%. Then the variables we have are P = 100000, M = 360, i = 0.084, N = 5, and g = 0.06. Plugging these values into the graduated payment formula gives us

100000/[(4.75505)(11.47138)+(0.88056)(125.23492)]
= 100000/164.82442
= 606.71.

For the first year, the monthly payments will be $606.71. To compute the payments in subsequent years, just multiply by 1.06 for each year, up to the 6th year:

Year 1: $606.71
Year 2: ($606.71)(1.06) = $643.11
Year 3: ($643.11)(1.06) = $681.70
Year 4: ($681.70)(1.06) = $722.60
Year 5: ($722.60)(1.06) = $765.96
Years 6-30: ($765.96)(1.06) = $811.92

For comparison, if you had a 30 year fixed rate mortgage at 8.4%, you would pay $761.84 each month. See the fixed rate mortgage calculator for more detail.

© Had2Know 2010