How to Figure the Number of Bricks for a Circular Border

Adding a brick border to a circular slab is an easy and cheap way to decorate indoor and outdoor fixtures. If you have a circular concrete pad in your yard, a brick border can help protect the edge of the circle. Indoors, many fireplaces have a semi-circular hearth that can be accented with a border of bricks.

To create a border from rectangular bricks, you arrange them around the circle so that the shorter sides are tangent to the edge of the circle.

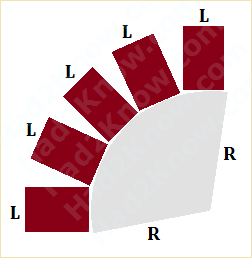
If the short side has length L and the circle has a radius of R, you can use these numbers to compute the maximum number of bricks that will fit around a whole circle. (To compute the max number of bricks for a semi-circular border, just divide by two.) The formula for the number of bricks is

Max # Bricks = π/[tan^-1(0.5L/R)]           radian formula

where the output of the function tan^-1 is in radians. If your calculator is set to degrees rather than radians, the equivalent formula is

Max # Bricks = 180/[tan^-1(0.5L/R)]           degree formula

Example 1: A circular concrete patio has a diameter of 16 feet, and you want to create a border with bricks that are 3 inches wide. What is the maximum number of bricks you can arrange around the outside edge of the patio?

Since the diameter is 16 feet, the radius is 8 feet. This is equivalent to 96 inches. So you have R = 96 and L = 3. Using the radian formula, you compute

Max # = π/[tan^-1(0.5*3/96)]
= π/[tan^-1(0.015625)]
= 3.1415926536 / 0.015623729
= 201.078291

The absolute maximum number of whole bricks you can fit around the border is 201. If you leave some space between the bricks, you need fewer.

Example 2: A semi-circular concrete patio has a diameter of 16 feet, and you want to create a border with bricks that are 3 inches wide, leaving a 1/4 inch space between bricks. How many bricks do you need?

In this example, R = 96 as before, but now L = 3.25. Using the radian formula, the number of bricks needed for a whole circle is

Max # = π/[tan^-1(0.5*3.25/96)]
= π/[tan^-1(0.016927083)]
= 3.1415926536 / 0.016925467
= 185.61335

The number required for a semi-circle is 185.61335/2, or about 92 whole bricks.

© Had2Know 2010