How to Figure the Number of Octagon and Square Tiles Needed

Although you cannot tile a surface using only regular octagons, you can create a seamless repeating pattern using octagons and squares. This is called a truncated square tiling, which is an example of a semi-regular tessellation. An octagon-and-square tiling pattern is a popular choice for indoor and outdoor flooring projects because it breaks up the monotony of a simple square pattern.

One of the most commonly asked questions when installing octagon and square tiles is how many tiles are needed. In such a pattern, one regular octagon is used for every square, so the total number of squares and octagons will be equal. To figure out what this number is, you can either follow the math steps below or use the calculator on the left.

To use the calculator on the left, you must enter the length of the side of a tile, the spacing between adjacent octagon tiles, and the total width and length of the space to be tiled. Since the octagon and square tiles are assumed to have the same side length, the spacing between two adjacent octagons will be slightly wider than the spacing between octagon and square. See the diagrams below for more detail.

Step 1: First compute the approximate amount of 2-dimensional space that each octagon-and-square unit occupy in the tile arrangement. If the side length of one tile is T inches and the spacing between adjacent octagon tiles is S inches, then the spacing between an octagon and square tile is S/√2. Using the formulas for the area of a square and regular octagon, the total amount of space they take up is

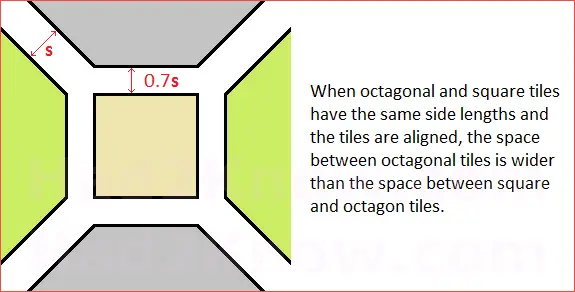
(2 + 2√2)[T + S/√2]² + [T + S/√2]² square inches
= (3 + 2√2)[T + S/√2]² square inches.

The expression above can be approximated by the simpler formula

Tile Area = 5.8(T + 0.7S)² in².

Step 2: Compute the area of the space you are going to tile, in square inches. This is done by calculating the square footage and then multiplying that number by 12*12 = 144. (The conversion factor for sq.ft to sq.in.) For a rectangular surface with a length of L feet and a width of W feet, the area is

144LW square inches.

Step 3: Divide the number you obtained in Step 2 by the number you obtained in Step 1. This is the exact number of octagon-square tile units you would need to cover the area, including any tiles that need to be cut, without any wasted tiles.

This does not give you the most realistic estimate for number of octagon and square tiles needed, since inevitably you will end up wasting some material. For a better estimate, add 5%-7% to this number.

Alternatively, you can add two tile side lengths to both the width and length in Step 2. For example, suppose the area to be tiled has a width of 15'4" and a length of 20'7", and suppose the side length of a tile is 5". Then the adjusted values of L and W are

L = 20'7" + 5" + 5" = 21'5"
W = 15'4" + 5" + 5" = 16'2"

This method is employed by the calculator above.

Example: You are tiling a floor space that is 14' wide and 22' long. You are using regular octagon and square tiles that have a side length of 3" and a spacing of 1/4" (0.25") between adjacent octagon tiles.

First, you use Step 1 to figure the amount of space each tile needs. This is approximately:

5.8(3 + 0.7*0.25)² = 58.46 in²

Next, the total square inches of the floor space to be tiled is 144*14*22 = 44352 in².

Now divide the first number into the second to compute the exact number of octagon-square tile units needed: 44352/58.46 = 759.

Finally, add about 6% more to this figure: 759 + 0.06*759 = 805. This means you need 805 square tiles and 805 octagon tiles, for a total of 1610 tiles.

© Had2Know 2010