Copyright © Had2Know 2010-2025. All Rights Reserved.
Terms of Use | Privacy Policy | Contact
Site Design by E. Emerson
Constructing Geometric Solids:
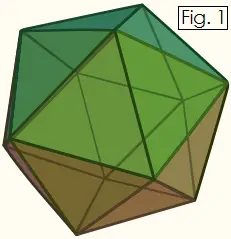
Icosahedron
The icosahedron is one of the five Platonic solids along with the cube, tetrahedron, octahedron and dodecahedron. A Platonic solid is one in which all the faces and vertices look the same. The 20 faces of an icosahedron are equilateral triangles that meet at five to a vertex. In geometry, the icosahedron is called the "dual" of the dodecahedron because each vertex of the icosahedron corresponds to a face of the dodecahedron, and vice versa.
With stiff paper, adhesive, pencil, and scissors or an Xacto knife, you can construct an icosahedron following the instructions below. You can use the icosahedron as a 20-sided die, or as a decoration.
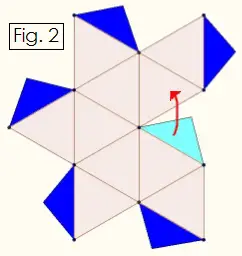
Repeat the above process for the Figure 3 below, which is the mirror image of Figure 2.
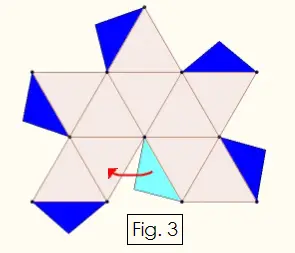
Fold all edges upward so that you make two halves of the solid figure. Notice that when you put the two shells together, you have ten dark blue tabs that interlock with ten triangles. Fit the blue tabs on one shell underneath the triangles on the other shell. Make sure that you have five triangles meeting at every point and glue the tabs in place. When the glue dries, you will have a complete icosahedron.
You can use gold and silver foil paper to make a mirror ball, use the figure as a 20-sided die, or use the pattern to build a piñata.
© Had2Know 2010
