Constructing Geometric Solids:
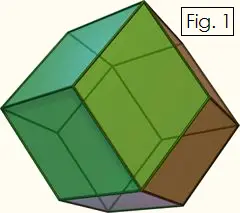
Rhombic Dodecahedron

A rhombic dodecahedron is a 12-sided solid shape in which every face is a rhombus, i.e., a quadrilateral with four sides of equal length, a diamond. One interesting property of rhombic dodecahedrons is that you can create a 3-dimensional tessellation with them, that is, you can pack them together with no gaps, just as you can do with cubes. The rhombic dodecahedron is also the dual of the cuboctahedron, since each vertex of the rhombic dodecahedron corresponds to a face of the cuboctahedron, and vice versa.

You can construct rhombic dodecahedrons out of stiff paper and glue (or clear tape) using the pattern and instructions that follow below. You will also need a ruler, pencil, and sharp scissors or an Xacto knife.

First, look at the Figure 1 on the right to see how a rhombic dodecahedron is built from rhombuses. The solid figure has 12 faces that meet at 14 points. Six of these points are where four diamonds meet, and eight of the points are where three diamonds meet.

You cannot construct a rhombic dodecahedron using just any kind of rhombus. Each face must have certain dimensions. The long diagonal and short diagonal must be in a ratio of sqrt(2) : 1 (or approximately 1.41421:1). The short diagonal and side must be in a ratio of 1 : sqrt(3)/2 (or approximately 1 : 0.866025). See Figure 2 on the left.

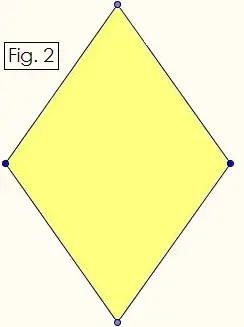
Using a ruler, sharp pencil, and the rhombus pattern in Figure 2, draw two copies of Figure 3 below. For each of these two of these figures, fold upward along every edge, and glue the light blue tabs onto the yellow rhombuses as indicated by the red arrows. You will then have two cup-like halves.

Make sure the dark blue tabs are folded toward the inside of the cups. Fit the two halves together where the obtuse angles of the diamonds match up. The dark blue tabs will be tucked inside. Once you see how the two halves of the rhombic dodecahedron fit together, glue the dark blue tabs to the rhombuses.

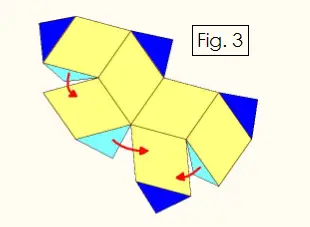
Once the glue on your solid shape has dried, you are done! Make several rhombic dodecahedrons and stack them like cubes without creating any gaps. You can also use these polyhedra as 12-sided dice.

© Had2Know 2010