How to Find the Major Axis, Minor Axis, and Foci of an Ellipse

Like a circle, an ellipse is a closed curve conic section. While a circle has infinitely many axes of symmetry, an ellipse has just two: the major axis and the minor axis. In addition to a geometric center, an ellipse has two special points called foci that lie along the major axis.

The foci of an ellipse are equidistant from the center and satisfy a special property: no matter which point you select on the border of the ellipse, if you draw a triangle connecting the point and each focus, the triangle's perimeter will remain the same.

If you are given an ellipse with the center point marked, you can use geometry to find the axes and the foci. You will need a ruler, straight edge, right angle, and either a pencil or string and tape to mark the lines. See also How to Find the Center of an Ellipse.

Finding the Axes

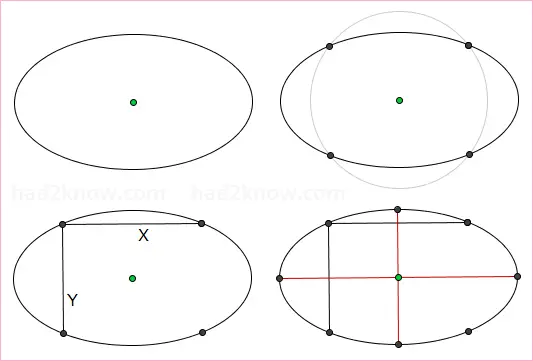
Step 1: Draw a circle that is centered at the ellipse's center and intersects the ellipse in four distinct points. Mark these points. The four points form the corners of rectangle inscribed within the ellipse.

Step 2: Use the straight edge and pencil to draw two perpendicular sides of this rectangle. Call these lines X and Y.

Step 3: Draw a line that passes through the center of the ellipse perpendicular to X and parallel to Y. This is one of the axes. Then draw a line that passes through the center perpendicular to Y and parallel to X. This is the other axis. The longer of the two axes is the major axis, while the shorter of the two is the minor axis. See figure below.

Finding the Foci

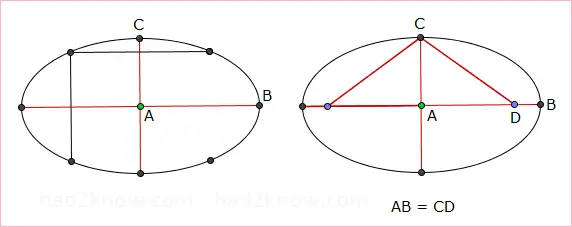
Step 1: Label the center of the ellipse A, one endpoint of the major axis B, and one endpoint of the minor axis C.

Step 2: Find a point D on the major axis such that the length of the segment from C to D equals the length from A to B. In other words, CD = AB. Since the major and minor axes cross at right angles, you also have the relation

CD = √AC² + AD²

The point D is one focus of the ellipse.

Step 3: Find the other focus using Step 2 again. See figure below.

© Had2Know 2010