Copyright © Had2Know 2010-2025. All Rights Reserved.
Terms of Use | Privacy Policy | Contact
Site Design by E. Emerson
Quarter Circle Arc Ellipse Approximation
In manufacturing and design it is often easier to create ellipse approximations rather than true ellipses. Several methods of creating pseudo-ellipses use circular arcs.
For example, two pairs of quarter circle arcs can be used to make a figure that looks very much like a true ellipse. The size difference between the arcs determines the shape's eccentricity.
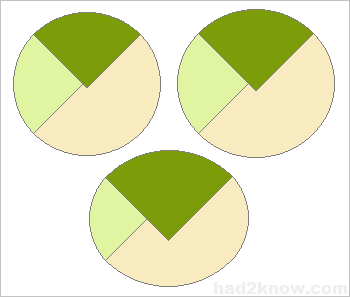
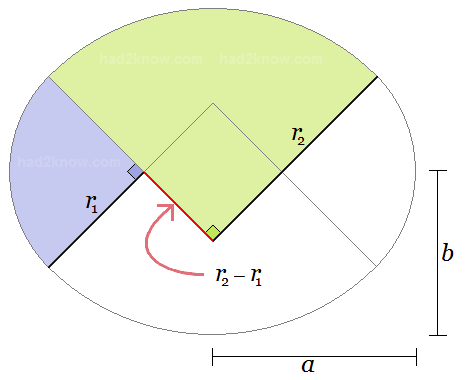
Likewise, if you know r2 and r1, you can solve for a and b. All of the necessary formulas are given below, or you can use the convenient calculator above.
Calculating r2 and r1 from a and b
Given dimensions a and b, where a ≥ b and a ≤ (1+√2)b, you can find the values of r2 and r1 as well as the perimeter and area with the equations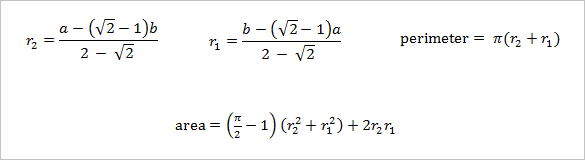
Calculating a and b from r2 and r1
Given r2 and r1, you can find the values of a and b as well as the perimeter and area with the equations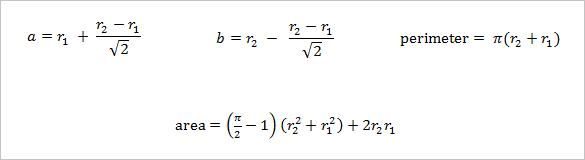
© Had2Know 2010
